Kurosaki
True Fail Kid
didn't have time to even reach it

Students helping students, join us in improving Bored of Studies by donating and supporting future students!
didn't have time to even reach it
I'm glad!this was by far my favourite question in any exam i have ever sat
Your proof is correct, and what I was looking for.I really have to ask why that circle geometry question is there at Question 16?
solution:
i) AMD is similar to CMB (AA)
Thus, CM/AM = CB/AD = CG/AF
And angle MCB = MAD (lol)
Thus FMA is similar to GMC (SAS)
ii) We know that OMX = OMY = 90 since M is midpoint of XY
So we just prove that POQ is isosceles.
construct lines OQ and MG, FM and PO
LEt angle MGC = MFA = alpha
Then angle MFO = MGO =90-alpha
which means that OPM = OQM = 90 - alpha
Thus the triangle POQ is isosceles and this means M bisects PQ since it's altitude.
Was this question there for free marks lol? Or was it put in because it's rather long (with all the reasoning and stuff)
I wanted some justification and also we were a bit more generous there to give the students a bit of a break =)also the other thing i didn't understand is why 14.b.i & ii were worth 2 marks each for like 30 seconds of work
did you time yourself?Hey all, I did the exam today at home. If anyone would like to compare or discuss answers, here are mine:
View attachment 31002.
I didn't include the three questions I drew diagrams for (two graphing q's and the circle geometry), I might do them in paint tomorrow lol...don't have a scanner.
I also didn't include every step of my working in this, so please ask if anything is unclear or if I just made sillies/typoes.
also 12b says z1z2 =/= -1 so it is trueHey all, I did the exam today at home. If anyone would like to compare or discuss answers, here are mine:
View attachment 31002.
I didn't include the three questions I drew diagrams for (two graphing q's and the circle geometry), I might do them in paint tomorrow lol...don't have a scanner.
I also didn't include every step of my working in this, so please ask if anything is unclear or if I just made sillies/typoes.
inb4 3 hoursdid you time yourself?
Not strictly, because I was latexing my answers as I did them (Including this time it took a little over 4 hours I think). I estimate I would have finished most but not all of the questions in 3 hours of strict exam conditions.did you time yourself?
oh woops didn't read your example right!isn't
though?
Do you remember your proof?oh woops didn't read your example right!
uh well i proved it in the exam but i guess there must be an exception.
in your example they still lie on the same line that passes through the origin but on opposite sides so the args differ by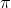
i did it with a drawing so not 100% positive. i think it only works if arg(z1)+arg(z2) < piDo you remember your proof?
Yeah, I know the args differ by...I cooked up that counterexample specifically to get the negative when I realised it was possible. I didn't bother examining the situation further to find out how numerous the counterexamples are (and whether or not the extent to which the claimed identity fails is constant.) I am kind of tired now, but I will look at it again tomorrow.
i did it with z2 in second quadrant and it was still fairly straightforward.Yeah, its definitely true and quite straightforward to show if they are both in the first quadrant. That was probably what was intended.
Lol appreciate the confidence, I am quite a bit better when doing problems in the comfort of my own room than in exam situations with pressure though so you probably overestimate me.i did it with z2 in second quadrant and it was still fairly straightforward.
if you don't state-rank 4U i will question this world.
Ps are you sure it works for z2 in second quadrant? If z1 is in the first quadrant but close to i and z2 is in the second quadrant and close to -1, I think the arguments still differ by pi.i did it with z2 in second quadrant and it was still fairly straightforward.
if you don't state-rank 4U i will question this world.
yeah that's why i mentioned arg(z1) + arg(z2) < pi as the condition before, i noticed that's the only way it worked with z2 in the second quadrantPs are you sure it works for z2 in second quadrant? If z1 is in the first quadrant but close to i and z2 is in the second quadrant and close to -1, I think the arguments still differ by pi.
I think that the geometric proof probably breaks when the arguments get big enough that z1z2 gets past -1 on the circle. So arg(z1) + arg(z2) < pi might be the best we could hope for.
Na still state rank.Lol appreciate the confidence, I am quite a bit better when doing problems in the comfort of my own room than in exam situations with pressure though so you probably overestimate me.
i constructed a quadrilateral using the points z, z+1, 1, and 0. and since it's a parallelogram, where the diagonal bisects the base angle, it must be a rhombus -> |z| = 1did anyone have a quick, neat way of doing 11 e) - the locus one with arguments
just curious, mine seems too dodgy...
