-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2014 MX2 Marathon ADVANCED (archive) (2 Viewers)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
So do you want a finite sum or infinite sum?what is the value of the infinite series, 1/1+ 1/2 +....+1/8+ 1/10 +...+1/18+ 1/20+.......
Btw this is the 1/1+1/2+1/3+....+1/n except without any terms with a 9 in the denominator
RealiseNothing
what is that?It is Cowpea
Re: HSC 2014 4U Marathon - Advanced Level
bro if you really think it's negative then good luckdo I detect sarcasm
Re: HSC 2014 4U Marathon - Advanced Level
It converges.So do you want a finite sum or infinite sum?
SilentWaters
Member
- Joined
- Mar 20, 2014
- Messages
- 55
- Gender
- Male
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
My bad. Question's asked incorrectly then.bro if you really think it's negative then good luck
ftfy(HSC Methods only)

FrankXie
Active Member
Re: HSC 2014 4U Marathon - Advanced Level
oh yep my badAlso I think the third line should read
FrankXie
Active Member
Re: HSC 2014 4U Marathon - Advanced Level
 )
actually u can't find the exact value it converges to.. Change the question to 'explain why the series converges and roughly where it converges'
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
Let be the set of reciprocals of k-digit positive integers that don't contain 9's.
be the set of reciprocals of k-digit positive integers that don't contain 9's.
Then the sum is
\cdot |S_k|=\sum_{k=1}^\infty 10^{-k+1}\cdot 8\cdot 9^{k-1}=8\sum_{k=1}^\infty (9/10)^{k-1}<\infty.)
The monotone convergence theorem completes the proof of convergence.
To obtain an accurate estimate, exactly sum the contributions of the first few S_k and use the same GP to bound the error. (This takes a while though, because 9/10 is pretty close to 1.)
Let
Then the sum is
The monotone convergence theorem completes the proof of convergence.
To obtain an accurate estimate, exactly sum the contributions of the first few S_k and use the same GP to bound the error. (This takes a while though, because 9/10 is pretty close to 1.)
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level

actually u can't find the exact value it converges to.. Change the question to 'explain why the series converges and roughly where it converges'
Re: HSC 2014 4U Marathon - Advanced Level
In trapezium (quadrilateral with one side parallel) with sides XY and ZU parallel, Angle UXY=6 degrees, Angle XYZ= 42 degrees. Point B is one side XY such that angle XBU = 78 degrees and angle ZBY = 66 degrees. If XY and Zu are 1 cm apart (vertically) prove that XU- YZ +UB-ZB = 8cm
In trapezium (quadrilateral with one side parallel) with sides XY and ZU parallel, Angle UXY=6 degrees, Angle XYZ= 42 degrees. Point B is one side XY such that angle XBU = 78 degrees and angle ZBY = 66 degrees. If XY and Zu are 1 cm apart (vertically) prove that XU- YZ +UB-ZB = 8cm
SilentWaters
Member
- Joined
- Mar 20, 2014
- Messages
- 55
- Gender
- Male
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
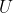 and
and 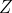 to
to 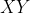 . From a consideration of the right angled triangles formed thereby, it should be easy trigonometry that
. From a consideration of the right angled triangles formed thereby, it should be easy trigonometry that ^{-1}, YZ = (sin\,42^{\circ})^{-1}, UB = (sin\,78^{\circ})^{-1}) and
and ^{-1}.) Plug these into the left-hand side and you have your eight.
Plug these into the left-hand side and you have your eight.
Drop perpendiculars fromIn trapezium (quadrilateral with one side parallel) with sides XY and ZU parallel, Angle UXY=6 degrees, Angle XYZ= 42 degrees. Point B is one side XY such that angle XBU = 78 degrees and angle ZBY = 66 degrees. If XY and Zu are 1 cm apart (vertically) prove that XU- YZ +UB-ZB = 8cm
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
Why does the n-th root of a number bigger than two have to be less than two? This doesn't look right to me.It should suffice to prove that each component of the sum exceedsBy the conditions,
so any
root of this where
should be less than two. It follows that the reciprocal must exceed a half.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
 because that does not seem to be a valid inference
because that does not seem to be a valid inference
At this part of your reasoning, are you saying that since:It should suffice to prove that each component of the sum exceedsBy the conditions,
so any
root of this where
should be less than two. It follows that the reciprocal must exceed a half.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
^{1/n}=((1+m)\cdot 1^{n-1})^{1/n}<\frac{m+n}{n})
by AM-GM. (Noting that not all terms are equal, so we cannot have equality.)
Similarly, we have
^{1/m}<\frac{m+n}{m}.)
Invert these inequalities and sum them to complete the proof.
by AM-GM. (Noting that not all terms are equal, so we cannot have equality.)
Similarly, we have
Invert these inequalities and sum them to complete the proof.
SilentWaters
Member
- Joined
- Mar 20, 2014
- Messages
- 55
- Gender
- Male
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
woah what the hell am I doing, wishful thinking. sorry guys, ignore that
woah what the hell am I doing, wishful thinking. sorry guys, ignore that
Axio
=o
- Joined
- Mar 20, 2014
- Messages
- 484
- Gender
- Male
- HSC
- 2015
Re: HSC 2014 4U Marathon - Advanced Level

Could you explain to me how you get that first line to fit the AM-GM inequality?
Noice.
by AM-GM. (Noting that not all terms are equal, so we cannot have equality.)
Similarly, we have
Invert these inequalities and sum them to complete the proof.
Could you explain to me how you get that first line to fit the AM-GM inequality?
Re: HSC 2014 4U Marathon - Advanced Level
how do you know that plugging those values into the LHS gives you 8 without using a calculator? You cannot use a calculator for this questionDrop perpendiculars fromand
to
. From a consideration of the right angled triangles formed thereby, it should be easy trigonometry that
and
Plug these into the left-hand side and you have your eight.
- Status
- Not open for further replies.

