HSC 2015 MX2 Integration Marathon (archive) (4 Viewers)

Drsoccerball · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Chlee1998 said:
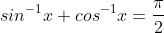
I doubt there's a solution for Ekman's question, although I might be wrong cause I didn't spend enough time on it

There is just try my question and then do his its genius
HINT: $sin^{-1}x +cos^{-1}x = \frac{\pi}{2}$

InteGrand · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Ekman said:
Here's a little twist to this question:

$\int_{0}^{1} (cos^{-1}x)^2 dx$

The integral can be written as $\int _0 ^1 \cos ^{-1} x \cdot \cos ^{-1}x \text{ d}x$ .

Replace $\cos ^{-1}x$ with $\frac{\pi}{2}-\sin ^{-1}x$ :

$I=\int _0 ^1 \left(\frac{\pi}{2}-\sin ^{-1}x \right)\cos ^{-1}x \text{ d}x$ .

Expand and break up the integral, using integration by parts on the first one and the answer to Drsoccerball's original integral for the second one.

Or, you don't need integration by parts for the first one, you can do it based on comparing the corresponding area to the inverse function.

swagswagyoloswag · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Ekman said:
Is the answer:
n!/(r+1)^n+1

how did you get a (r+1)^(n+1) at the bottom? I got a (r+1)^n
I_n = -n/(r+1)I_n-2 so I_n-1 = -(n-1)/(r+1)I_n-3 and so on. didn't get a n+1

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

swagswagyoloswag said:
how did you get a (r+1)^(n+1) at the bottom? I got a (r+1)^n
I_n = -n/(r+1)I_n-2 so I_n-1 = -(n-1)/(r+1)I_n-3 and so on. didn't get a n+1

I counted I_0 which is just 1/r+1 , so that's the extra +1. Maybe I might be wrong because I have trouble visualising how many times it gets multiplied.

swagswagyoloswag · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Ekman said:
I counted I_0 which is just 1/r+1 , so that's the extra +1

I only had a (r+1)^n-1 and then multiplied with I_0

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

swagswagyoloswag said:
I only had a (r+1)^n-1 and then multiplied with I_0

What was your I_n? Mine was: $I_{n}=\frac{-n}{r+1} I_{n-1}$

The way I see it for the denominator is that I_0=1/r+1. Hence I_1 = 1/(r+1)^2, I_2=2/(r+1)^3 ... I_n=n!/(r+1)^n+1 (Note, I ignored the minus one for the sake of demonstrating how i got the (r+1)^n+1)

swagswagyoloswag · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Ekman said:
What was your I_n? Mine was: $I_{n}=\frac{-n}{r+1} I_{n-1}$

The way I see it for the denominator is that I_0=1/r+1. Hence I_1 = 1/(r+1)^2, I_2=2/(r+1)^3 ... I_n=n!/(r+1)^n+1 (Note, I ignored the minus one for the sake of demonstrating how i got the (r+1)^n+1)

Mine was the same. So
$-I_n = \frac{n}{r+1}I_{n-1}$

$-I_{n-1} = \frac{n-1}{r+1}I_{n-2}$

$-I_{n-2} = \frac{n-2}{r+1}I_{n-3}$
.
.
.
$-I_1 = \frac{1}{r+1}I_{0}$

$-I_0 = \frac{1}{r+1}$
I multiplied 2nd eqn. by $\frac{n}{r+1}$ then subtract from eqn. above and multiplied 3rd eqn by $\frac{n(n-1)}{r+1}$ and added and so forth. So for $I_{n-1}$ it would have a fraction of $\frac{n}{r+1}$ while $I_{n-2}$ had $\frac{n(n-1)}{(r+1)^2}$ so the pattern for the denominator is $(r+1)^{n-c}$ where c = subscript of I. So $I_1$ will have denominator of n-1 while $I_0$ has a denominator of n? Idk if there was something wrong with it

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

swagswagyoloswag said:
Mine was the same. So
$-I_n = \frac{n}{r+1}I_{n-1}$

$-I_{n-1} = \frac{n-1}{r+1}I_{n-2}$

$-I_{n-2} = \frac{n-2}{r+1}I_{n-3}$
.
.
.
$-I_1 = \frac{1}{r+1}I_{0}$

$-I_0 = \frac{1}{r+1}$
I multiplied 2nd eqn. by $\frac{n}{r+1}$ then subtract from eqn. above and multiplied 3rd eqn by $\frac{n(n-1)}{r+1}$ and added and so forth. So for $I_{n-1}$ it would have a fraction of $\frac{n}{r+1}$ while $I_{n-2}$ had $\frac{n(n-1)}{(r+1)^2}$ so the pattern for the denominator is $(r+1)^{n-c}$ where c = subscript of I. So $I_1$ will have denominator of n-1 while $I_0$ has a denominator of n? Idk if there was something wrong with it

Im not sure how you got C to be the representation of the subscript of I when n is the that representation. And if the denominator is: $(r+1)^{n-c}$ then I_n would have a denominator as 1, basically cancelling out the r+1

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Next Question:

$\int \sin^{-1}x \cdot ln(x) dx$

Drsoccerball · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Ekman said:
Next Question:

$\int \sin^{-1}x \cdot ln(x) dx$

$$ IBM with letting $ u=lnx $ and $ dv=sin^{-1}x$

$lnx \cdot sin^{-1}x \cdot x+ \sqrt{1-x^2} \cdot lnx - \int{sin^{-1}x +\frac{\sqrt{1-x^2}}{x}}$

$lnx \cdot sin^{-1}x \cdot x+ \sqrt{1-x^2} \cdot lnx -xsin^{-1}x -\sqrt{1-x^2} - \int{\frac{\sqrt{1-x^2}}{x}}$

$$ let $ x = cos\theta$

$\int{\frac{-sin^2{\theta}}{cos\theta}}$

$\int{-sec\theta +cos\theta}$

$= -ln(sec\theta +tan\theta) +sin\theta$

Simplify this and add it to the long thing

Drsoccerball · Apr 26, 2015

Re: MX2 2015 Integration Marathon

NEW QUESTION
$Given $ I_n= \int_0^1x^n \cdot 2^x dx $ Show that:$

$I_n = \frac{2}{ln2} - \frac{n}{ln2}I_{n-1}$

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Drsoccerball said:
NEW QUESTION
$Given $ I_n= \int_0^1x^n \cdot 2^x dx $ Show that:$

$I_n = \frac{2}{ln2} - \frac{n}{ln2}I_{n-1}$

$$Via IBP: $ \frac{d}{dx} \left(\frac{x^n\cdot 2^x}{ln2} \right) - \frac{n}{ln2} x^{n-1} 2^x =x^n \cdot 2^x$

$\therefore I_{n} = \left[\frac{x^n\cdot 2^x}{ln2} \right]_{0}^{1} - \frac{n}{ln2} I_{n-1}$

$= \frac{2}{ln2} - \frac{n}{ln2}I_{n-1}$

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Next Question:

$\int \frac{x^2-1}{x\sqrt{x^4+1}} dx$

VBN2470 · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Ekman said:
Next Question:

$\int \frac{x^2-1}{x\sqrt{x^4+1}} dx$

Use the substitution $$u = x + \frac{1}{x}$$ .

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Next Question:

$\int \frac{\sin^2x}{\cos^2x+\cot^2x} dx$

WhoStanLeee · Apr 26, 2015

Re: MX2 2015 Integration Marathon

VBN2470 · Apr 26, 2015

Re: MX2 2015 Integration Marathon

^ Your method is correct, but you shouldn't be mixing u's with x's, keep your variable the same throughout as your manipulating the integrand as this is not mathematically sound which could result in a loss of marks in the HSC exam.

WhoStanLeee · Apr 26, 2015

Re: MX2 2015 Integration Marathon

Yeah, it does look a bit strange...how would I go about undergoing the substitution in one line though? To prevent having u's and x's at the same time?

Ekman · Apr 26, 2015

Re: MX2 2015 Integration Marathon

I used the substitution $x=\sqrt{\tan\theta}$

And I was left with: $\frac{1}{2} \int \sec(\theta)-\csc(\theta) d\theta$

InteGrand · Apr 26, 2015

Re: MX2 2015 Integration Marathon

VBN2470 said:
^ Your method is correct, but you shouldn't be mixing u's with x's, keep your variable the same throughout as your manipulating the integrand as this is not mathematically sound which could result in a loss of marks in the HSC exam.

There's surely nothing wrong with that, e.g. in the volume integration formula, we often write $V=\pi \int _a ^b y^2 \text{ d}x$ .

His u is a function of x, he's just doing an algebraic manipulation

WhoStanLeee said:
Yeah, it does look a bit strange...how would I go about undergoing the substitution in one line though? To prevent having u's and x's at the same time?

To reduce chances of markers taking off marks (which they shouldn't, but very well may), you could explicitly write $u(x)$ instead of $u$ to remind them it's a function of x.

HSC 2015 MX2 Integration Marathon (archive) (4 Viewers)

Well-Known Member

Well-Known Member

Member

Well-Known Member

Member

Well-Known Member

Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Member

Well-Known Member

Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 4)