To see why using
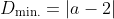
for
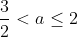
is optimal, note that the squared distance function represents a concave up parabola. Therefore, it is minimised at its vertex, and as we saw before, this globally minimising
x-value is
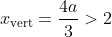
as
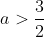
. So the parabola is minimised at a point where
x > 2, so the closest we can get to this minimal value by taking a point on the ellipse is to make
x on the ellipse closest to this value greater than 2, which is clearly by taking
x = 2, and this point (the point (2,0)) on the ellipse has distance to the point (
a, 0) of
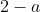
, which is the same as
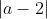
as required.
(And we noted earlier that the optimal distance for
a > 2 was
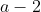
, which is equal to
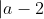
, so in either case
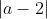
is optimal.)
, satisfying the condition
.
.
