Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
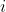 xcosx \leq sinx \leq x $ for very small positive values )
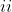 \lim_{x \to 0} 1 \leq \lim_{x \to 0}\frac{sinx}{x} \leq 1 )

My teachers way of explaining squeeze theorem:
"If eating a burger and theres cheese in it, you will always eat the cheese"
My teachers way of explaining squeeze theorem:
"If eating a burger and theres cheese in it, you will always eat the cheese"
Last edited:

