-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Graphing the derivative HSC question (1 Viewer)
- Thread starter BlueGas
- Start date
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
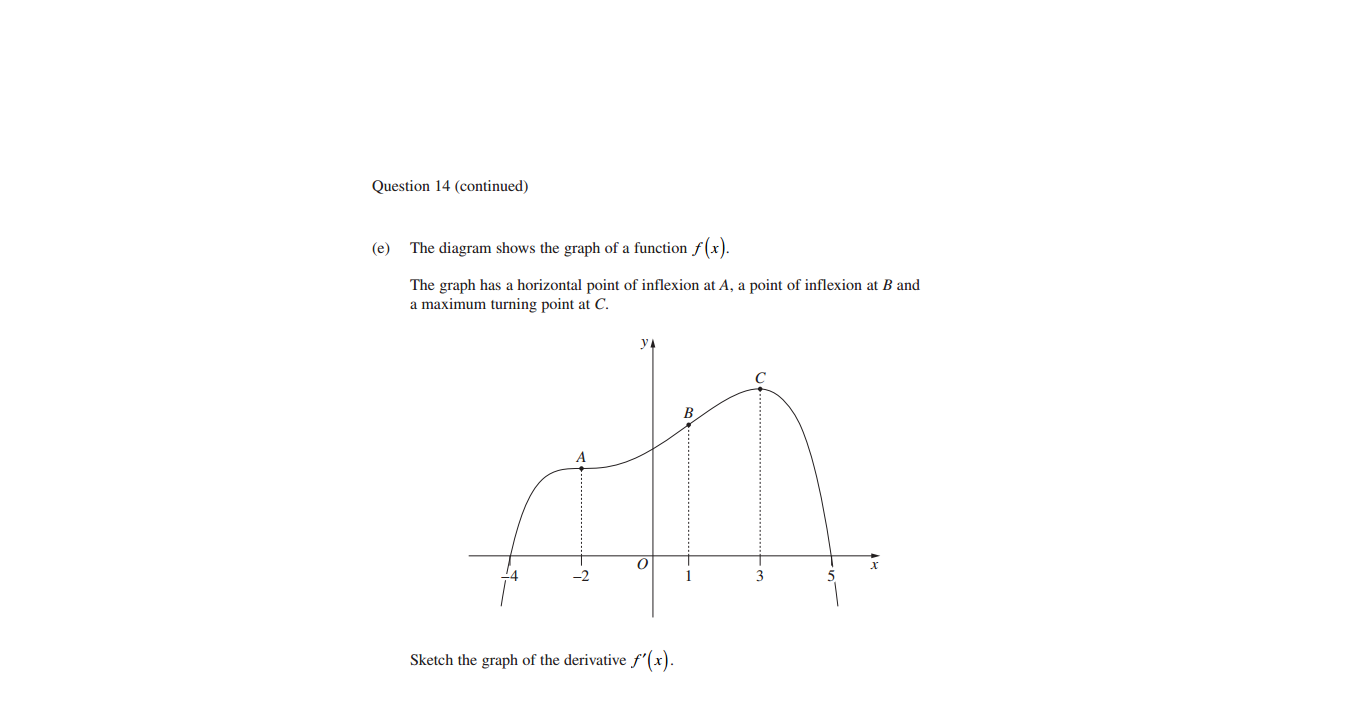
When differentiating a function turning points become x intercepts and inflection points become turning point. So considering this in the domain ofI need help with this question, I have no clue how to start so I need to know the basics.
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
Just a quick bump, since inflection points become stationary/turning points, how'd you know that x= -2 it's a minimum and at x= 1 there's another minimum?When differentiating a function turning points become x intercepts and inflection points become turning point. So considering this in the domain of
the function start from positive infinity y axis (Since gradient appears to be infinitely positive) and is going down till -2. So as mentioned before stationary points become intercepts and inflection points become turning points therefore there would be a minimum stationary point at x=-2. So the graph then increases untill a min turning point at x=1. At x=3 it crosses the x axis and continues downwards
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Because you look at the gradient before and after it:Just a quick bump, since inflection points become stationary/turning points, how'd you know that x= -2 it's a minimum and at x= 1 there's another minimum?
Its increasing and the after the point it decrease. The only point that does that is a max turning point
Just a quick bump, since inflection points become stationary/turning points, how'd you know that x= -2 it's a minimum and at x= 1 there's another minimum?
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
Wait so it's a maxiumum? You said max turning point? I thought it was a minimum?Because you look at the gradient before and after it:
Its increasing and the after the point it decrease. The only point that does that is a max turning point
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
Also you said at x = 1 there's a minimum, but the actual answer has x = 1 as a maximum.When differentiating a function turning points become x intercepts and inflection points become turning point. So considering this in the domain of
the function start from positive infinity y axis (Since gradient appears to be infinitely positive) and is going down till -2. So as mentioned before stationary points become intercepts and inflection points become turning points therefore there would be a minimum stationary point at x=-2. So the graph then increases untill a min turning point at x=1. At x=3 it crosses the x axis and continues downwards
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
Okay so to the left of x = -2 is a max and to the right is a min, so how did you conclude that it's a minimum when sketching the derivative?
Sorry, yeah, local maximum for f' at x = 1, because the derivative of f' is positive to the left of it (that is, f"(x) > 0 just to the left of 1, as the curve is concave up there) and the derivative of f' is negative to the right of x = 1 (as the concanvity there is concave down).Okay so to the left of x = -2 is a max and to the right is a min, so how did you conclude that it's a minimum when sketching the derivative?
Okay so to the left of x = -2 is a max and to the right is a min, so how did you conclude that it's a minimum when sketching the derivative?
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
That's the problem, my teacher NEVER touched on this topic, it's unbelievable, as a result I'm having a hard time understanding this graphing the derivative and so on. I only have a vague idea on this.
So far what I've learnt, not only from this question, but other questions is that:
f(x) is if the point is positive or negative, basically if the graph is above the x axis or not, for example at say (-2, 3) f(x) > 0 however if it was (-2, -2) it would instead be f(x) < 0
f'(x) is the slope/gradient, if it's positive or negative
f''(x) is if it's a max or a min
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
On the most left, f(x) appears to be increasing, that is, f'(x) >0. The concavity of f (x) is also negative, so f''(x) <0. That means for the f'(x) curve, the derivative (ie. The gradient) of that curve is also negative since f"(x)<0. So we can say that the f '(x) starts positive (above the x axis) and decreases downAlso how do I know where the graph starts from? From top or bottom?
Last edited:
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
Ah okay, so when f''(x) < 0, then the gradient is a negative and starts from the top?On the most left, f(x) appears to be increasing, that is, f'(x) >0. The concavity of f (x) is also negative, so f''(x) <0. That means for the f'(x) curve, the derivative (ie. The gradient) of that curve is also negative since f"(x)<0. So we can say that the f '(x) starts positive (above the x axis) and decreases down
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
If f"(x)<0 then the gradient of y = f'(x) is negative. For the y = f (x), it only tells us that it has a negative concavity (think, a concave down parabola). It only starts at the top for the y=f'(x) curve because for y=f (x), the gradient (and hence f'(x)) is positive.Ah okay, so when f''(x) < 0, then the gradient is a negative and starts from the top?
.
.
.
So it starts at top b/c gradient of f (x) is positive and it has a negative gradient because f''(x) is negative
You can try graphing the first derivative, and then use this graph to graph the second derivative.Since this is only finding the first derivative, what are the steps I should take to find the second derivative?
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
What InteGrand said.
But if you're able to, you might be able to draw the second derivative from the y = f(x) graph by assessing the concavities at each point.
eg. from x = -infinity to x = -2,
the concavity is highly negative, until it reaches x = -2 where there's an inflexion point, showing us that f''(x) = 0. Then after this point, the concavity is positive.
So you can represent this on a graph, starting at x=-infinity, f''(x) = very negative and it goes up until x= -2 where it crosses the x-axis and continues going up and becomes positive because the concavity of f(x) after x = -2 is positive
But if you're able to, you might be able to draw the second derivative from the y = f(x) graph by assessing the concavities at each point.
eg. from x = -infinity to x = -2,
the concavity is highly negative, until it reaches x = -2 where there's an inflexion point, showing us that f''(x) = 0. Then after this point, the concavity is positive.
So you can represent this on a graph, starting at x=-infinity, f''(x) = very negative and it goes up until x= -2 where it crosses the x-axis and continues going up and becomes positive because the concavity of f(x) after x = -2 is positive
Also note that the given graph looks like that of a quartic (fourth degree polynomial), so we would expect the first derivative graph to look like that of a cubic, and the second derivative graph to look like that of a quadratic.
