-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
asdfghjklqwerty
Member
- Joined
- Sep 14, 2015
- Messages
- 33
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
can someone do part ii please
can someone do part ii please
Paradoxica
-insert title here-
Re: HSC 2015 4U Marathon
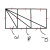
Ohohoho, I remember doing this question. The tension in the second scenario is 11 newtons...A 3 metre string AB has a mass of 5kg attached at point B. The string is rotated in a horizontal circle about A and breaks as soon as it exceeds a speed of rotation of 45 revolutions per minute.
i.Find the maximum possible tension in the string.
ii. the mass at B is replaced by a 3kg mass and an additional 1kg mass is attached to the string at C, 2 metres from A (as shown below). Find the new maximum number of revolutions per minute that the string can be rotated.
i need help with part ii now( thanks
ans: 52.5revs/minute
asdfghjklqwerty
Member
- Joined
- Sep 14, 2015
- Messages
- 33
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
can u tell me how to do it??
can u tell me how to do it??
Paradoxica
-insert title here-
Re: HSC 2015 4U Marathon
I barely understand how forces interact between objects, sorry man. That's just what I got. The tension exerted by the 1 kg mass should be 2 N and the tension exerted by the 3kg mass should be 9 N. You need to use your own understanding of tension to justify that.
I barely understand how forces interact between objects, sorry man. That's just what I got. The tension exerted by the 1 kg mass should be 2 N and the tension exerted by the 3kg mass should be 9 N. You need to use your own understanding of tension to justify that.
Zlatman
Member
- Joined
- Nov 4, 2014
- Messages
- 73
- Gender
- Male
- HSC
- 2015
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
[video]https://youtube.com/watch?v=m5evLoL0xwg[/video]
This is a classic problem and has something like 50+ different known solutions iirc. One classic solution is via reflecting the diagram, and is shown in a Numberphile video (linked below). (Can also solve via inverse trig., requires an inverse trig. addition identity).View attachment 32500
Find alpha + beta + gamma
All squares are of side lengths 1.
There's a way using complex numbers
[video]https://youtube.com/watch?v=m5evLoL0xwg[/video]
Last edited:
Re: HSC 2015 4U Marathon
Geez... such creativityThis is a classic problem and has something like 50+ different known solutions iirc. One classic solution is via reflecting the diagram, and is shown in a Numberphile video (linked below). (Can also solve via inverse trig., requires an inverse trig. addition identity).
[video]https://youtube.com/watch?v=m5evLoL0xwg[/video]
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
I saw that one and the complex number one which I liked lol. arg((i+1)(i+2)(i+3)) = arg(10i) = pi/2
I saw that one and the complex number one which I liked lol. arg((i+1)(i+2)(i+3)) = arg(10i) = pi/2
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
Here's an easy one to kickstart this marathon again:

Here's an easy one to kickstart this marathon again:
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon

^{2} )
 )









Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon
Lol, De Moivre's theorem is usually proved USING the trig addition formulae. This is quite circular.Here's an easy one to kickstart this marathon again:

Re: HSC 2015 4U Marathon
Only the limited version involving integer powers.Lol, De Moivre's theorem is usually proved USING the trig addition formulae. This is quite circular.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon
A full statement of the theorem is then slightly clunkier, but could still be obtained by using the integer power version to obtain the rational power version, and using the continuity of the trig functions to extend this to the reals.
Anyway, this is a digression. The version of De Moivres used in answering this question is only required to treat integer powers, and any proof of this version of De Moivres either explicitly uses the trig addition formulae or proves this fact in disguise.
Well when we stop talking about integer power we start getting multivalued.Only the limited version involving integer powers.
A full statement of the theorem is then slightly clunkier, but could still be obtained by using the integer power version to obtain the rational power version, and using the continuity of the trig functions to extend this to the reals.
Anyway, this is a digression. The version of De Moivres used in answering this question is only required to treat integer powers, and any proof of this version of De Moivres either explicitly uses the trig addition formulae or proves this fact in disguise.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon
I don't think those conditions uniquely determine ab + cd...
Paradoxica
-insert title here-
Re: HSC 2015 4U Marathon
| = 1 \Rightarrow bc-ad = 1) (actually, ab+cd is multivalued... checked using W|A)
(actually, ab+cd is multivalued... checked using W|A)
Last edited:
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
There's only one solution for ab + cdI don't think those conditions uniquely determine ab + cd...
- Status
- Not open for further replies.