Re: HSC 2016 4U Marathon - Advanced Level
Yep yep I screwed up hahahaYou're thinking of the factorisation of (t+h)^q + t^q
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Yep yep I screwed up hahahaYou're thinking of the factorisation of (t+h)^q + t^q
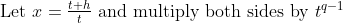
Suppose that it is Easter weekend coming up, so that Friday and Monday are both public holidays (i.e. 4 day weekend).
John wants to go to the beach on exactly one day of the long weekend (so Friday, Saturday, Sunday, Monday).
However he wants to go on the hottest day of the long weekend.
Assuming that John is rational, and that he only finds out the temperature a particular day will be at 9am of the day itself (and so can only decide if he wants to go to the beach at 9am on that day), what is the probability that John goes to the beach on the hottest day as he wants to?
(Assume the temperature on any of the 4 days is completely random and not dependent on other factors such as the previous temperature etc. Also assume the temperature can not be the same on any of the 4 days to avoid ties).
Pretty much this.
Yeah but wouldn't it need to have a finite max. (and min.) temp.? A uniform distribution on an infinite support doesn't make sense.Pretty much this.
Forget about any physical restrictions on max/min temperatures though. Think of it as say a God just choosing the temperature to be whatever the first number that comes to his mind is (so I guess it would be uniformally distributed).
Yep.Yeah but wouldn't it need to have a finite max. (and min.) temp.? A uniform distribution on an infinite support doesn't make sense.
I guess you essentially mean that whatever the temperature is on a day, the next day's one is equally likely to be above it as below it (and can't equal it).
This may or may not be completely wrong and/or based on a misinterpretation of the question
------
Pr(John picks the right day) =
Pr(John picks the first day, and it is the hottest the second day) +
Pr(John picks the second day, and it is the hottest the second day) +
Pr(John picks the third day, and it is the hottest the third day) +
Pr(John picks the fourth day, and it is the hottest the fourth day)
= 1/4*1/4 + 1/4*1/2 + 1/4*3/4 + 1/4 * 1 = 5/8
At the start of the first day, to him, every day is equally possible for it to be the hottest day, so the probability he picks it is 1/4, and the probability the first is the hottest is 1/4 (non-epistemic)
At the start of the second day, depending on how the first day went, it might be rational for John to not go the second day at all (i.e. if T2 < T1)
Given that John does pick the second day, the probability that it is the hottest is 1/2. This is because:
There are 24 different orderings of temperature (which I will denote by the numbers 1, 2, 3, 4, the lower the number the lower the temperature)
(e.g. if the order is: 1, 4, 3, 2, it means that 2nd day is hottest followed by day 3, then day 4 then day 1)
There are 24 = 4! orderings, 12 of these orderings are such that 2nd day is greater than 1, and of these 6 of them are such that 2nd day = 4
Thus 6/12 = 1/2
Similarly for the 3rd day, of the 24 orderings, there are 8 orderings so that the 3rd is the hottest out of the first 3 days
Of these 8, there are 6 that are such that 3rd day is indeed the hottest day,
Thus Pr(3rd is hottest) given John picks 3rd day is 6/8 = 3/4
Similarly for day 4 it is 1
-------
Your logic is right, but the probability is wrong I think.
I did 1 minus the probability that all 3 of the next days are colder than Day 1 (given that it is Day 1 currently). Is this the wrong way to calculate that probability?Your logic is right, but the probability is wrong I think.
Wouldn't it just be 1/4 chance that day 1 is the hottest (we have no information on any other days yet), so 3/4 chance that it isn't?I did 1 minus the probability that all 3 of the next days are colder than Day 1 (given that it is Day 1 currently). Is this the wrong way to calculate that probability?
Lol idk, maybe this is the new Monty Hall haha.Wouldn't it just be 1/4 chance that day 1 is the hottest (we have no information on any other days yet), so 3/4 chance that it isn't?
I understand how you got that probability though and now I'm kinda mind-fucked.
That's the same instinct I had whilst thinking about why we get two different probabilities. Might look into it a bit more since it seems way more counter-intuitive than even the Monty Hall problem.Lol idk, maybe this is the new Monty Hall haha.
I have a feeling that before Day 1, the chance that Day 1 is hottest is 1/4, but once you know Day 1's temperature on Day 1, it changes to 1/8?? Or maybe this is a problem with having the infinite uniform distribution. Or maybe it's like the Envelope paradox thing. Actually, remembering this paradox, I think the following is true: if the four days' temperatures are fixed beforehand (by an omniscient genie say), then the probability is indeed 3/4. But if they're not fixed and truly can be higher or lower than Day 1 on each later day with 50-50 chance, then the probability should be the one calculated above (0.875).
I think the answer to this problem will be different if we consider the temperature as NOT fixed beforehand (which is how I interpreted it) compared to if they were fixed, haven't thought of it in much detail, this is kinda based on my instinct and the relation to the envelope paradox.
Still not quite right...in your (**) line, substituting z=0 would give p(t)= p(0) + At^qM(0).Revamping solution (and making some of the inferences more rigorous), had fun writing this
-----------
-----------
-----------------
 means that at HSC level at least, this at most finds all$ \ \textbf{real} \ $polynomials with the aforementioned properties$ )

