HSC 2016 MX2 Marathon (archive) (2 Viewers)

Sy123 · Nov 10, 2015

Re: HSC 2016 4U Marathon

KingOfActing said:
$i) Solving the equations simultaneously we obtain $ \alpha = \frac{ikm}{m+i}$, $ \beta = \frac{k}{m+i}$ and as such $ z = \alpha \ +\ \beta = \frac{ikm + k}{m + i} = \frac{(ikm+k)(m-i)}{m^2 + 1} = \frac{ikm^2 + km + km - ik}{m^2 + 1} = \frac{2mk}{m^2 + 1} + i\frac{m^2-1}{m^2 + 1}k $ as required.$\\\\$By making the substitution $m = \tan{\frac{\frac{\pi}{2} - \theta}{2}}$ and using the t-formulae, our expression for $z$ becomes $ k\sin{\left(\frac{\pi}{2} - \theta\right)} + ik\cos{\left (\frac{\pi}{2} - \theta\right)} = k(\cos{\theta} \ +\ i\sin{\theta}) $ which is the polar form of any complex number.$

Well done

--------

A more intuitive way of approaching part (ii) especially is to ask, "what does it mean for every complex number to be represented?"

Essentially, it just means that every complex number's argument and modulus can be represented, and the domains for both are not restricted.

Looking at the modulus of z, we see:

$|z|^2 = \left(\frac{2mk}{m^2+1}\right)^2 + \left(\frac{(m^2-1)k}{m^2+1}\right)^2 \\ \\ \Rightarrow \ |z| = \frac{k^2}{(m^2+1)^2} (4m^2 + (m^2-1)^2) = k^2$

$\\ $So,$ \ |z| = k$

$\\ $This means that$ \ |z| $can vary freely as we can freely select$ \ k \ $so that our desired complex number's modulus is gotten by letting$ \ k \ $equal that desired modulus$$

$\\ $Letting the argument of the complex number be$ \ \theta \ $we see that$ \ \cos \theta = \frac{2m}{m^2+1}$

$\\ $No matter what our desired complex number's argument is, the cosine of that angle must lie between -1 and 1 inclusive$$

$\\ $This means that if we can find a real$ \ m \ $so that the equation holds true for some$ \ -1 \leq \cos \theta \leq 1$

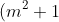$\\ (m^2+1) \cos \theta = 2m \\ \Rightarrow \ m^2 \cos \theta - 2m + \cos \theta = 0$

$\\ $The discriminant of the quadratic is$ \ 4 - 4\cos^2 \theta = 4\sin^2 \theta \geq 0$

$\\ $This means that there always exists a real$ \ m \ $so that$ \ \cos \theta = \frac{2m}{m^2+1} \ $for any given$ \ \theta$

$\\ $This means with appropriate selection of$ \ m \ $and$ \ k \ $one can independently find any desired modulus and argument, thus any complex number can be represented$$

Drsoccerball · Nov 11, 2015

Re: HSC 2016 4U Marathon

$(i)After Sy123's continuous solutions Integrand became jealous. Having played many mathematical games in the past he decided to play another one, but this time it was with Sy123's life!$

$Integrand told Sy123 to come to his own private pit in which he would regularly throw Biology and English teachers in. He gave Sy123 a smile and said ''stand at the edge.''$

$Sy123 looked down and with his hawk-like vision and saw that the bottom had 5 spikes evenly distributed such that if he happened to fall in they would all penetrate his body. Integrand kicked Sy123 in the chest sending him flying horizontally.$

$$ Assuming the Height which is not spiked is $ \frac{R}{2} $ Where R is the total distance of the pit. Prove the time it takes to reach the spikes is $ T= \frac{1}{2\sqrt{gk}}ln{|\frac{\sqrt{\frac{g}{k}-\frac{ge^{Rk}}{k}}-\sqrt{\frac{g}{k}}}{\sqrt{\frac{g}{k}-\frac{ge^{Rk}}{k}}+\sqrt{\frac{g}{k}}}|} $given that the air resistance is $ kmv^2$

$(ii) Assuming the total journey is J seconds and the resistance provided by each spike is W, Find the height of the pit.$

Ekman · Nov 11, 2015

Re: HSC 2016 4U Marathon

Drsoccerball said:
$(i)After Sy123's continuous solutions Integrand became jealous. Having played many mathematical games in the past he decided to play another one, but this time it was with Sy123's life!$

$Integrand told Sy123 to come to his own private pit in which he would regularly through Biology and English teachers in. He gave Sy123 a smile and said ''stand at the edge.''$

$Sy123 looked down and with his hawk-like vision and saw that the bottom had 5 spikes evenly distributed such that if he happened to fall in they would all penetrate his body. Integrand kicked Sy123 in the chest sending him flying horizontally.$

$$ Assuming the Height which is not spiked is $ \frac{R}{2} $ Where R is the total distance of the pit. Prove the time it takes to reach the spikes is $ T= \frac{1}{2\sqrt{gk}}ln{|\frac{\sqrt{\frac{g}{k}-\frac{ge^{Rk}}{k}}-\sqrt{\frac{g}{k}}}{\sqrt{\frac{g}{k}-\frac{ge^{Rk}}{k}}+\sqrt{\frac{g}{k}}}|} $given that the air resistance is $ kmv^2$

$(ii) Assuming the total journey is J seconds and the resistance provided by each spike is W, Find the height of the pit.$

Just to give a visual representation of this:

porcupinetree · Nov 11, 2015

Re: HSC 2016 4U Marathon

Drsoccerball said:
$(i)After Sy123's continuous solutions Integrand became jealous. Having played many mathematical games in the past he decided to play another one, but this time it was with Sy123's life!$

$Integrand told Sy123 to come to his own private pit in which he would regularly through Biology and English teachers in. He gave Sy123 a smile and said ''stand at the edge.''$

$Sy123 looked down and with his hawk-like vision and saw that the bottom had 5 spikes evenly distributed such that if he happened to fall in they would all penetrate his body. Integrand kicked Sy123 in the chest sending him flying horizontally.$

$$ Assuming the Height which is not spiked is $ \frac{R}{2} $ Where R is the total distance of the pit. Prove the time it takes to reach the spikes is $ T= \frac{1}{2\sqrt{gk}}ln{|\frac{\sqrt{\frac{g}{k}-\frac{ge^{Rk}}{k}}-\sqrt{\frac{g}{k}}}{\sqrt{\frac{g}{k}-\frac{ge^{Rk}}{k}}+\sqrt{\frac{g}{k}}}|} $given that the air resistance is $ kmv^2$

$(ii) Assuming the total journey is J seconds and the resistance provided by each spike is W, Find the height of the pit.$

Leaked Question 8(b) of 2016 Ext 2 HSC??

leehuan · Nov 11, 2015

Re: HSC 2016 4U Marathon

Drsoccerball said:
$Integrand told Sy123 to come to his own private pit in which he would regularly through Biology and English teachers in. He gave Sy123 a smile and said ''stand at the edge.''$

Nice grammar.

Drsoccerball · Nov 11, 2015

Re: HSC 2016 4U Marathon

leehuan said:
Nice grammar.

You make questions then

leehuan · Nov 11, 2015

Re: HSC 2016 4U Marathon

Drsoccerball said:
You make questions then

I only throw in rote learnt stuff because most 2016ers aren't that far into the course yet!

Drsoccerball · Nov 13, 2015

Re: HSC 2016 4U Marathon

Here's an easier one:

$$(i) Integrand realises he is being chased by the police. He sees a round about ahead of him and has a thought. ''What speed would I need to go in order to not have any friction''$

$This roundabout is banked at an angle of $ \theta $ and the road starts at the centre of the roundabout. Integrand travels at G meters from the bottom of the roundabout.$

$$ Prove that his velocity is $ v=\sqrt{Ggsin\theta}$

Sy123 · Nov 14, 2015

Re: HSC 2016 4U Marathon

For questions of an appropriate difficulty and beyond the capabilities of most current 2016er 4U students (at this stage in which they only know Complex Numbers/Polynomials), take it to the Advanced Thread.

-----------------------

This is at a reasonable difficulty (Q13-14)

$\\ $Let$ \ z \ $be a complex number so that$ \ z^5 - 1 \\ \\ $i) Explain why$ \ 1+z+z^2+z^3+z^4= \left(z^2 - 2z\cos \frac{2\pi}{5} + 1 \right) \left(z^2 - 2z\cos \frac{4\pi}{5} + 1 \right)$

$\\ $ii) Show that$ \ \left(1 - \cos \frac{2\pi}{5} \right) \left(1 - \cos \frac{4\pi}{5} \right) = \frac{5}{4} \ $and that,$ \\\\ \left(\frac{5}{4} - \cos \frac{2\pi}{5} \right) \left(\frac{5}{4} - \cos \frac{4\pi}{5} \right) = \frac{31}{16}$

$\\ $iii) Using the previous two equations, find the quadratic equation with roots$ \ \cos \frac{2\pi}{5} \ $and$ \ \cos \frac{4\pi}{5}$

$\\ $iv) Find, using your equation from part (iii) the quadratic equation with roots$ \ \cos^2 \frac{2\pi}{5} \ $and$ \ \cos^2 \frac{4\pi}{5}$

$\\ $v) Show that$ \ \cos^8 \frac{2\pi}{5} + \cos^8 \frac{4\pi}{5} = \frac{47}{256}$

leehuan · Nov 14, 2015

Re: HSC 2016 4U Marathon

Sy123 said:
Question

z^5-1=0 you mean?

Anyway, hints for ACTUAL 2016ers:
(i) Look at the question. What even are the values for z? Also, you should have been taught any 4u factorisation methods.
(ii)There are multiple ways of doing this, but if you're dumbfounded a simple (however potentially exhaustive, I haven't tried it out) method just uses a bit of Yr 11 3U...
(iv) Not as hard as it seems. ^2
(highlight)

Ambility · Nov 14, 2015

Re: HSC 2016 4U Marathon

Sy123 said:
$\\ $Let$ \ z \ $be a complex number so that$ \ z^5 - 1 \\ \\ $i) Explain why$ \ 1+z+z^2+z^3+z^4= \left(z^2 - 2z\cos \frac{2\pi}{5} + 1 \right) \left(z^2 - 2z\cos \frac{4\pi}{5} + 1 \right)$

$\\ $ii) Show that$ \ \left(1 - \cos \frac{2\pi}{5} \right) \left(1 - \cos \frac{4\pi}{5} \right) = \frac{5}{4} \ $and that,$ \\\\ \left(\frac{5}{4} - \cos \frac{2\pi}{5} \right) \left(\frac{5}{4} - \cos \frac{4\pi}{5} \right) = \frac{31}{16}$

$\\ $iii) Using the previous two equations, find the quadratic equation with roots$ \ \cos \frac{2\pi}{5} \ $and$ \ \cos \frac{4\pi}{5}$

$\\ $iv) Find, using your equation from part (iii) the quadratic equation with roots$ \ \cos^2 \frac{2\pi}{5} \ $and$ \ \cos^2 \frac{4\pi}{5}$

$\\ $v) Show that$ \ \cos^8 \frac{2\pi}{5} + \cos^8 \frac{4\pi}{5} = \frac{47}{256}$

Thank you for posting a question which is within the scope of this year's cohort. I enjoyed doing this one.

$$i) By polynomial division: $z^5-1=(z-1)(z^4+z^3+z^2+z+1)\\$The roots of $z^5-1$ are: $z=1, cis\frac{2\pi}{5}, cis\frac{-2\pi}{5}, cis\frac{4\pi}{5}, cis\frac{-4\pi}{5}\\$Therefore $z^5-1$ can be factorised as $(z-1)(z-cis\frac{2\pi}{5})(z-cis\frac{-2\pi}{5})(z-cis\frac{4\pi}{5})(z-cis\frac{-4\pi}{5})\\$Equating: $(z-1)(z^4+z^3+z^+2+z+1)=(z-1)(z-cis\frac{2\pi}{5})(z-cis\frac{-2\pi}{5})(z-cis\frac{4\pi}{5})(z-cis\frac{-4\pi}{5})\\(z^4+z^3+z^+2+z+1)=(z-cis\frac{2\pi}{5})(z-cis\frac{-2\pi}{5})(z-cis\frac{4\pi}{5})(z-cis\frac{-4\pi}{5})\\(z^4+z^3+z^+2+z+1)=(z^2-2\cos{\frac{2\pi}{5}}+1)(z^2-2\cos{\frac{4\pi}{5}}+1)$

$$ii) $(1-\cos{\frac{2\pi}{5}})(1-cos{\frac{4\pi}{5}})=1-\cos{\frac{2\pi}{5}}-cos{\frac{2\pi}{5}}+\cos{\frac{2\pi}{5}}cos{\frac{2\pi}{5}}\\$Equating $z^2$ parts from above equation: $z^2=z^2+z^2+4\cos{\frac{2\pi}{5}}\cos{\frac{4\pi}{5}}z^2\\1=2+4\cos{\frac{2\pi}{5}}\cos{\frac{4\pi}{5}}\\\cos{\frac{2\pi}{5}}\cos{\frac{4\pi}{5}}=-\frac{1}{4}\\$Equating z parts from above equation: $z=-2\cos{\frac{2\pi}{5}}z-2\cos{\frac{4\pi}{5}}z\\-\cos{\frac{2\pi}{5}}-\cos{\frac{4\pi}{5}}=\frac{1}{2}\\$Substituting these into the original equation for ii: $\\1+\frac{1}{2}-\frac{1}{4}=\frac{5}{4}$

$$ii) $(1-\cos{\frac{2\pi}{5}})(1-cos{\frac{4\pi}{5}})=1-\cos{\frac{2\pi}{5}}-cos{\frac{2\pi}{5}}+\cos{\frac{2\pi}{5}}cos{\frac{2\pi}{5}}\\$Equating $z^2$ parts from above equation: $z^2=z^2+z^2+4\cos{\frac{2\pi}{5}}\cos{\frac{4\pi}{5}}z^2\\1=2+4\cos{\frac{2\pi}{5}}\cos{\frac{4\pi}{5}}\\\cos{\frac{2\pi}{5}}\cos{\frac{4\pi}{5}}=-\frac{1}{4}\\$Equating z parts from above equation: $z=-2\cos{\frac{2\pi}{5}}z-2\cos{\frac{4\pi}{5}}z\\-\cos{\frac{2\pi}{5}}-\cos{\frac{4\pi}{5}}=\frac{1}{2}\\$Substituting these into the original equation for ii: $\\1+\frac{1}{2}-\frac{1}{4}=\frac{5}{4}$

$$iii) Roots $\alpha$ and $\beta$ are $\cos{\frac{2\pi}{5}}$ and $\cos{\frac{4\pi}{5}}\\x^2-(\alpha+\beta)+\alpha\beta =0\\x^2-\frac{1}{2}x-\frac{1}{4}=0$

$$iv) Make an equation with roots $\alpha^2$ and $\beta^2\\\alpha^2+\beta^2=(\alpha+\beta)^2-2\alpha\beta\\=(-\frac{1}{2})^2-2(\frac{-1}{4})\\=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\\$Equation: $x^2-\frac{3}{4}x+\frac{1}{16}$

$$v) Wow, this one took a while.$\\\cos^8{\frac{2\pi}{5}}+\cos^8{\frac{4\pi}{5}}=\alpha^8+\beta^8$
$$By binomial expansion: $(\alpha+\beta)^8=\alpha^8+8\alpha^7\beta+28\alpha^6\beta^2+56\alpha^5\beta^3+70\alpha^4\beta^4+56\alpha^3\beta^5+28\alpha^2\beta^6+8\alpha\beta^7+\beta^8$

$\alpha^8+\beta^8=(\alpha+\beta)^8-8\alpha^7\beta-28\alpha^6\beta^2-56\alpha^5\beta^3-70\alpha^4\beta^4-56\alpha^5\beta^3-28\alpha^6\beta^2-8\alpha\beta^7\\=\frac{1}{256}-8(\alpha\beta)\alpha^6-28(\alpha^2\beta^2)a^4-56(\alpha^3\beta^3)\alpha^2-70(\frac{1}{256})-56(\alpha^3\beta^3)\beta^2-28(\alpha^2\beta^2)\beta^4-8(\alpha\beta)\beta^6$

$=-\frac{69}{256}+2(\alpha^6+\beta^6)-\frac{7}{4}(\alpha^4+\beta^4)+\frac{7}{8}(\alpha^2+\beta^2)\\\alpha^2+\beta^2=\frac{3}{4}\\\alpha^4+\beta^4=(\alpha^2+\beta^2)^2-2\alpha^2\beta^2\\=\frac{9}{16}-2(\frac{1}{16})\\=\frac{7}{16}$
$\alpha^6+\beta^6=(\alpha^2+\beta^2)^3-3\alpha^4\beta^2-3\alpha^2\beta^4\\=\frac{27}{64}-\frac{3}{16}(\alpha^2+\beta^2)\\=\frac{9}{32}$
$\frac{-69}{256}+2(\frac{9}{32})-\frac{7}{4}(\frac{7}{16})+\frac{7}{8}(\frac{3}{4})=\frac{47}{256}$

Ambility · Nov 14, 2015

Re: HSC 2016 4U Marathon

NEXT QUESTION for anyone in the 2016 cohort:

$$Use de Moivre's theorem to express $\cos{6\theta}$ as a polynomial in terms of \cos{\theta}.$
HINT IF NEEEDED (highlight): You will need to use the binomial expansion for a binomial of 6th degree.

Paradoxica · Nov 14, 2015

Re: HSC 2016 4U Marathon

Sy123 said:
For questions of an appropriate difficulty and beyond the capabilities of most current 2016er 4U students (at this stage in which they only know Complex Numbers/Polynomials), take it to the Advanced Thread.

-----------------------

This is at a reasonable difficulty (Q13-14)

$\\ $Let$ \ z \ $be a complex number so that$ \ z^5 - 1 \\ \\ $i) Explain why$ \ 1+z+z^2+z^3+z^4= \left(z^2 - 2z\cos \frac{2\pi}{5} + 1 \right) \left(z^2 - 2z\cos \frac{4\pi}{5} + 1 \right)$

$\\ $ii) Show that$ \ \left(1 - \cos \frac{2\pi}{5} \right) \left(1 - \cos \frac{4\pi}{5} \right) = \frac{5}{4} \ $and that,$ \\\\ \left(\frac{5}{4} - \cos \frac{2\pi}{5} \right) \left(\frac{5}{4} - \cos \frac{4\pi}{5} \right) = \frac{31}{16}$

$\\ $iii) Using the previous two equations, find the quadratic equation with roots$ \ \cos \frac{2\pi}{5} \ $and$ \ \cos \frac{4\pi}{5}$

$\\ $iv) Find, using your equation from part (iii) the quadratic equation with roots$ \ \cos^2 \frac{2\pi}{5} \ $and$ \ \cos^2 \frac{4\pi}{5}$

$\\ $v) Show that$ \ \cos^8 \frac{2\pi}{5} + \cos^8 \frac{4\pi}{5} = \frac{47}{256}$

$Although this has been done by Ambility, I will post my own solution.$

$i) As the factorisations of $z^5 - 1$ are identical, we can compare factors. Since $(z-1)$ is common to both sides, it follows that the remaining four factors form the same polynomial. -Insert complex argument for co-efficients here-$

$ii) After substituting $z = 1, z = \frac{1}{2}$ and simplifying, we have the desired results$

$iii) Replace $\cos{\frac{2\pi}{5}}$ with $\alpha$ and $\cos{\frac{4\pi}{5}}$ with $\beta$. Expanding out the identities from ii) yield:$

$1 - \left ( \alpha + \beta \right ) + \alpha \beta = \frac{5}{4}$

$\frac{25}{16} - \frac{5}{4} \left ( \alpha + \beta \right ) + \alpha \beta = \frac{31}{16}$

$Solving simultaneously for $\alpha + \beta$ and $\alpha \beta$ yields:$

$\alpha + \beta = -\frac{1}{2}, \alpha \beta = -\frac{1}{4}$

$$The desired quadratic has the roots $\alpha , \beta$

$Q(z) = (z-\alpha)(z-\beta) = z^2 - (\alpha + \beta)z + \alpha \beta = z^2 + \frac{z}{2} - \frac{1}{4} = 0$

$iv) To acquire the quadratic with roots $\alpha^2, \beta^2, $ replace $z$ with \sqrt{z}.$

$z + \frac{\sqrt{z}}{2} -\frac{1}{4} = 0$

$\sqrt{z} = \frac{1}{2} \left ( 1 - 4z \right )$

$z = \frac{16z^2 - 8z + 1}{4}$

$R(z) = z^2 - \frac{3}{4} z + \frac{1}{16} = 0$

$$with $\alpha^2 + \beta^2 = \frac{3}{4}$ and $\alpha^2\beta^2 = \frac{1}{16}$

$$v) $\alpha^8 + \beta^8 = \left ( \alpha^4 + \beta^4 \right )^2 - 2\alpha^4 \beta^4 = \left ( \left ( \alpha^2 + \beta^2 )^2 - 2\alpha^2 \beta^2 \right ) \right )^2 - 2(\alpha^2 \beta^2)^2 = \left ( \left (\frac{3}{4} \right )^2 - \frac{1}{8} \right)^2 - \frac{1}{128} = \frac{47}{256}$

Ambility · Nov 14, 2015

Re: HSC 2016 4U Marathon

Paradoxica said:
$Although this has been done by Ambility, I will post my own solution.$

$i) As the factorisations of $z^5 - 1$ are identical, we can compare factors. Since $(z-1)$ is common to both sides, it follows that the remaining four factors form the same polynomial. -Insert complex argument for co-efficients here-$

$ii) After substituting $z = 1, z = \frac{1}{2}$ and simplifying, we have the desired results$

$iii) Replace $\cos{\frac{2\pi}{5}}$ with $\alpha$ and $\cos{\frac{4\pi}{5}}$ with $\beta$. Expanding out the identities from ii) yield:$

$1 - \left ( \alpha + \beta \right ) + \alpha \beta = \frac{5}{4}$

$\frac{25}{16} - \frac{5}{4} \left ( \alpha + \beta \right ) + \alpha \beta = \frac{31}{16}$

$Solving simultaneously for $\alpha + \beta$ and $\alpha \beta$ yields:$

$\alpha + \beta = -\frac{1}{2}, \alpha \beta = -\frac{1}{4}$

$$The desired quadratic has the roots $\alpha , \beta$

$Q(z) = (z-\alpha)(z-\beta) = z^2 - (\alpha + \beta)z + \alpha \beta = z^2 + \frac{z}{2} - \frac{1}{4} = 0$

$iv) To acquire the quadratic with roots $\alpha^2, \beta^2, $ replace $z$ with \sqrt{z}.$

$z + \frac{\sqrt{z}}{2} -\frac{1}{4} = 0$

$\sqrt{z} = \frac{1}{2} \left ( 1 - 4z \right )$

$z = \frac{16z^2 - 8z + 1}{4}$

$R(z) = z^2 - \frac{3}{4} z + \frac{1}{16} = 0$

$$with $\alpha^2 + \beta^2 = \frac{3}{4}$ and $\alpha^2\beta^2 = \frac{1}{16}$

$$v) $\alpha^8 + \beta^8 = \left ( \alpha^4 + \beta^4 \right )^2 - 2\alpha^4 \beta^4 = \left ( \left ( \alpha^2 + \beta^2 )^2 - 2\alpha^2 \beta^2 \right ) \right )^2 - 2(\alpha^2 \beta^2)^2 = \left ( \left (\frac{3}{4} \right )^2 - \frac{1}{8} \right)^2 - \frac{1}{128} = \frac{47}{256}$

Why does replacing z with root z yield a quadratic with roots of $\alpha^2$ and $\beta^2$ ?

InteGrand · Nov 14, 2015

Re: HSC 2016 4U Marathon

Ambility said:
Why does replacing z with root z yield a quadratic with roots of $\alpha^2$ and $\beta^2$ ?

$This is the typical method of finding a polynomial equation with roots $\alpha^2$ etc. when given a polynomial with roots $\alpha$ etc. You'll learn it later in the HSC 4U Polynomials topic when you get to it. The reason it works is that replacing $z$ with $\sqrt{z}$ and later squaring both sides means that roots of the new equations are squares of the old one.$

$That is, if $\alpha_1,\alpha_2,\ldots,\alpha_n$ are the roots of an $n$th degree polynomial equation $P(z)=0$, then an $n$th degree polynomial equation is obtained by replacing $z$ with $\sqrt{z}$ and rearranging and \textsl{squaring both sides} (typically to eliminate the square roots, although if only even terms are present, the square roots aren't present and the purpose is to get the polynomial to the right degree and get the new polynomial's roots to the right multiplicity, since if the original polynomial has only even terms, its roots come in $\pm$ pairs, so the polynomial with roots which are squares of the original's, the roots come in even multiplicities). The rearranged polynomial is an $n$th degree polynomial with roots $\alpha_1^2,\alpha_2^2,\ldots,\alpha_n^2$.$

$We can make this into a question:$

$Let $P(z)$ be an $n$th degree polynomial with zeros $\alpha_1,\alpha_2,\ldots,\alpha_n \in \mathbb{C}$. Show that the polynomial equation formed by rearranging $P\left(\sqrt{z}\right)=0$ by grouping all square root terms on one side and then \textsl{squaring both sides} and rearranging, calling this new equation $Q(z)=0$, has roots $\alpha_1^2, \alpha_2^2,\ldots, \alpha_n^2$ (assume that $n\geq 2$).$

Paradoxica · Nov 15, 2015

Re: HSC 2016 4U Marathon

InteGrand said:
$This is the typical method of finding a polynomial equation with roots $\alpha^2$ etc. when given a polynomial with roots $\alpha$ etc. You'll learn it later in the HSC 4U Polynomials topic when you get to it. The reason it works is that replacing $z$ with $\sqrt{z}$ and later squaring both sides means that roots of the new equations are squares of the old one.$

$That is, if $\alpha_1,\alpha_2,\ldots,\alpha_n$ are the roots of an $n$th degree polynomial equation $P(z)=0$, then an $n$th degree polynomial equation is obtained by replacing $z$ with $\sqrt{z}$ and rearranging and \textsl{squaring both sides} (typically to eliminate the square roots, although if only even terms are present, the square roots aren't present and the purpose is to get the polynomial to the right degree and get the new polynomial's roots to the right multiplicity, since if the original polynomial has only even terms, its roots come in $\pm$ pairs, so the polynomial with roots which are squares of the original's, the roots come in even multiplicities). The rearranged polynomial is an $n$th degree polynomial with roots $\alpha_1^2,\alpha_2^2,\ldots,\alpha_n^2$.$

$We can make this into a question:$

$Let $P(z)$ be an $n$th degree polynomial with zeros $\alpha_1,\alpha_2,\ldots,\alpha_n \in \mathbb{C}$. Show that the polynomial equation formed by rearranging $P\left(\sqrt{z}\right)=0$ by grouping all square root terms on one side and then \textsl{squaring both sides} and rearranging, calling this new equation $Q(z)=0$, has roots $\alpha_1^2, \alpha_2^2,\ldots, \alpha_n^2$ (assume that $n\geq 2$).$

$$Further more, to generalise the statement, if you want a polynomial with roots $f(z)$, then simplify $P(f^{-1}(z))$ and you will have the relevant polynomial. However, this only works iff $f: \mathbb C \rightarrow \mathbb C$ is bijective. Or If you're working in $\mathbb R$, then $f: \mathbb R \rightarrow \mathbb R$. Similarly for $\mathbb Z .$

InteGrand · Nov 15, 2015

Re: HSC 2016 4U Marathon

Paradoxica said:
$Further more, to generalise the statement, if you want a polynomial with roots $f(z)$, then simplify $P(f^{-1}(z))$ and you will have the relevant polynomial. However, this only works iff $f$ is bijective.$

$For the case of squared roots, even though $x^2$ is not bijective, using $P\left(\sqrt{z} \right)$ and then rearranging etc. works, despite this being just one branch of the inverse relation, which is a \textsl{multivalued function}. The crucial part is the \textsl{squaring both sides} part, which takes care of things.$

$(The use of $\sqrt{z}$ in those parts is actually an abuse of notation actually; when we use it for these polynomial questions, we use it to just mean anything whose square is $z$; in other words, a sort of multi-valued object; in general it is invalid to square both sides of something, but when we do it in these polynomials questions, we are really thinking of the $\sqrt{z}$ as multivalued. It doesn't really matter once we do square both sides. And the equation that results will have roots being the squares of the roots of the original polynomial.)$

$For a simple example, if we had a polynomial equation $x+1 = 0$, with root $\alpha = -1$, and wanted the polynomial of degree one with root $\alpha^2 = 1$, we would do this:$

$\begin{align*}\sqrt{x}+1&= 0 \\ \sqrt{x} &= -1 \quad (\text{grouping the square root terms to one side (note that this line is ordinarily bogus, as the square root symbol refers to the positive root if it is real, so can't be negative!)}) \\ x &= 1 \quad (\textsl{squaring both sides (ordinarily bogus)})\\ x-1 &= 0.\end{align*}$

$Therefore, the desired polynomial equation is $x-1=0$ (as expected!). So it is best to think of the $\sqrt{x}$ symbol in this context as a multivalued object. Maybe it'd be better to use a new notation to denote it, e.g. $_{\pm}\sqrt{x}$.$

Paradoxica · Nov 15, 2015

Re: HSC 2016 4U Marathon

InteGrand said:
$For the case of squared roots, even though $x^2$ is not bijective, using $P\left(\sqrt{z} \right)$ and then rearranging etc. works, despite this being just one branch of the inverse relation, which is a \textsl{multivalued function}. The crucial part is the \textsl{squaring both sides} part, which takes care of things.$

$$What would happen if I had something like a new polynomial with roots $2^x ?$

InteGrand · Nov 15, 2015

Re: HSC 2016 4U Marathon

Paradoxica said:
$$What would happen if I had something like a new polynomial with roots $2^x ?$

$I'm guessing in general it's too much to hope to find a \emph{polynomial} equation with those roots or with arbitrary function of the original roots, with our standard HSC 4U methods anyway. Of course, we can do this when the roots are $\sqrt{\alpha}$ or $\alpha^{3}$ etc. because the resultant equations involve powers of $x$ still so the equation will be polynomial, or can be made so by squaring etc. We can still form \emph{an} equation though with those roots of course, by making the replacement $x\mapsto \log_2 x$ in the original equation.$

Paradoxica · Nov 15, 2015

Re: HSC 2016 4U Marathon

$i) If $f(x)$ is convex and positive, prove $e^{f(x)}$ is convex.$

$ii) Disprove the converse statement.$

HSC 2016 MX2 Marathon (archive) (2 Viewers)

This too shall pass

Well-Known Member

Well-Known Member

not actually a porcupine

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

This too shall pass

Well-Known Member

Active Member

Active Member

-insert title here-

Active Member

Well-Known Member

-insert title here-

Well-Known Member

-insert title here-

Well-Known Member

-insert title here-

Users Who Are Viewing This Thread (Users: 0, Guests: 2)