Need help, URGENT maths question: (2 Viewers)

leehuan · Apr 24, 2016

1008 said:
Hey leehuan. Yes, I am doing MATH1151. Do you mean the red booklet? I can't find the answers in the purple booklet anywhere....

The red one has answers before the past quiz papers to some selected problems. That was one of the few proofs it chose to give.

InteGrand · Apr 24, 2016

1008 said:
Thanks. There is this question that's been bugging me for a while now.
$\\\text{(a) A container in the shape of a right circular cone, of semi-vertical angle }\tan^{-1}{\frac{1}{2}}\text{,}\\\text{ is placed vertex downward with its axis vertical. Water is poured in at the rate of }10mm^{3}\text{ per}\\\text{sec. Find the rate at whice the depth, }h\text{ mm, is increasing when the depth of water in the }\\\text{cone is }50mm. \\\\\text{The cone is filled to a depth of 100mm and pouring is then stopped. A hole is then}\\\text{at the vertex of the cone and water flows out of the hole at the rate of }50\sqrt{h}\text{ }{mm}^{3}\\\text{ per second,where }h\text{ is the depth at time }t.\text{Show that it takes 200s to empty the cone.}$

I get part (a). The answer is $\frac{2}{125\pi}$ . But the answer to part (b) that I get is 166.67 seconds.

For part b), we are given dV/dt in terms of h. We can also find dV/dh in terms of h using geometry. So we can use the chain rule to get dh/dt as a function of h, f(h). So dt will be dh/f(h). So you can find the required time by integrating the RHS from h = 0 to 100.

1008 · Apr 24, 2016

leehuan said:
The red one has answers before the past quiz papers to some selected problems. That was one of the few proofs it chose to give.

Thanks, found it. I was referring to the purple booklet. But that is literally the only proof they've given in the answers.

BTW any thoughts on the cone question?

InteGrand · Apr 24, 2016

1008 said:
Thanks, found it. I was referring to the purple booklet. But that is literally the only proof they've given in the answers.

BTW any thoughts on the cone question?

I put up a method above. Is that the method you were using? If not, what did you do?

1008 · Apr 24, 2016

InteGrand said:
I put up a method above. Is that the method you were using? If not, what did you do?

Sorry InteGrand, I was replying to leehuan's question. And after I posted it, I saw your reply. I was actually using a different (and incorrect method). I've put it below:

$\frac{dt}{dV}=\frac{-1}{50\pi\sqrt{h}}\\\therefore\int_{0}^{t}dt = \frac{-1}{50\pi\sqrt{h}}\int_{\frac{100^{3}\pi}{12}}^{0}dV\\\text{Substituting }h = 100mm\text{, we get }t={166}\frac{2}{3} \approx 166.67$

But I can see why it's incorrect now. This was one of various approaches that got me different answers.

1008 · Apr 24, 2016

Hey everyone, I've got another question.

$\\\text{(a) (i) Show that the polynomial }p_{3}\text{ where }p_{3}(x) = 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!},\text{ has}\text{ at least one real root}\\\text{(ii) Show that the polynomial }p_{2}\text{ where }p_{2}(x) = 1+x+\frac{x^{2}}{2},\text{ has no real roots and}\\\text{deduce that }p_{3}\text{ has exactly one real root.}\\\text{(iii) Deduce that }p_{4}(x) = 1+x+\frac{x^{2}}{2}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}>0\text{ for all real numbers }x.$ I get the first two parts of the question, just need help with the third part.

InteGrand · Apr 24, 2016

1008 said:
Hey everyone, I've got another question.

$\\\text{(a) (i) Show that the polynomial }p_{3}\text{ where }p_{3}(x) = 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!},\text{ has}\text{ at least one real root}\\\text{(ii) Show that the polynomial }p_{2}\text{ where }p_{2}(x) = 1+x+\frac{x^{2}}{2},\text{ has no real roots and}\\\text{deduce that }p_{3}\text{ has exactly one real root.}\\\text{(iii) Deduce that }p_{4}(x) = 1+x+\frac{x^{2}}{2}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}>0\text{ for all real numbers }x.$ I get the first two parts of the question, just need help with the third part.

Note that p₄'(x) = p₃(x) for all x. Also, p₄"(x) = p₂(x) for all x. We've shown that p₂(x) is a positive definite quadratic, so that means the second derivative of p₄ is always positive. This means the minimum of p₄ will be a global min.

Now, to find this min., set p₄'(x) = p₃(x) = 0. (There is exactly one solution to this, as you've shown in a previous part.)

But observe that p₄(x) = p₃(x) + x⁴/4!. So at the point where p₄'(x) ≡ p₃(x) = 0, say at x = a, we have p₄(a) = 0 + a⁴/4! > 0 (strictly positive since clearly a is not zero, because p₃ doesn't have its root at 0).

So the absolute minimum value of p₄(x) is positive. Hence p₄(x) > 0 for all real x.

1008 · Apr 24, 2016

InteGrand said:
Note that p₄'(x) = p₃(x) for all x. Also, p₄"(x) = p₂(x) for all x. We've shown that p₂(x) is a positive definite quadratic, so that means the second derivative of p₄ is always positive. This means the minimum of p₄ will be a global min.

Now, to find this min., set p₄'(x) = p₃(x) = 0. (There is exactly one solution to this, as you've shown in a previous part.)

But observe that p₄(x) = p₃(x) + x⁴/4!. So at the point where p₄'(x) ≡ p₃(x) = 0, say at x = a, we have p₄(a) = 0 + a⁴/4! > 0 (strictly positive since clearly a is not zero, because p₃ doesn't have its root at 0).

So the absolute minimum value of p₄(x) is positive. Hence p₄(x) > 0 for all real x.

The way I did it was I just chose an arbitrary interval [-25,0] and just went from there. Here's my working:
$\\\text{(a) (i) As }p_{3}(x) = 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}\text{ is a polynomial it is both continuous and differentiable}\\\text{everywhere. }\\\therefore\text{ We can apply the Intermediate Value Theorem. Suppose we apply the IVT over [-25,0]}\\p_{3}(-25) = \frac{-6943}{3}<0, p_{3}(0) =1>0\\\therefore\text{ There is at least one c}\in\text{ }[-25,0]\text{ such that }p_{3}=0.\\\\\text{(ii) }p_{2}(x) = 1+x+\frac{x^{2}}{2}\\\Delta = b^{2}-4ac = -1<0\\\therefore\text{No real solution to }p_{2}(x)\\\text{Now }p_{3}'(x) = 1+x+\frac{x^{2}}{2!} = p_{2}(x)\text{ which has no solution. Hence p3 has no turning points}\\\therefore\text{Using part (i) }p_{3}(x)\text{ has only one zero, in the interval [-25,0]}.$

So how would your explanation to part iii continue on from my working for the first two parts?

leehuan · Apr 24, 2016

1008 said:
The way I did it was I just chose an arbitrary interval [-25,0] and just went from there. Here's my working:
$\\\text{(a) (i) As }p_{3}(x) = 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}\text{ is a polynomial it is both continuous and differentiable}\\\text{everywhere. }\\\therefore\text{ We can apply the Intermediate Value Theorem. Suppose we apply the IVT over [-25,0]}\\p_{3}(25) = \frac{-6943}{3}<0, p_{3}(0) =1>0\\\therefore\text{ There is at least one c}\in\text{ }[-25,0]\text{ such that }p_{3}=0.\\\\\text{(ii) }p_{2}(x) = 1+x+\frac{x^{2}}{2}\\\Delta = b^{2}-4ac = -1<0\\\therefore\text{No real solution to }p_{2}(x)\\\text{Now }p_{3}'(x) = 1+x+\frac{x^{2}}{2!} = p_{2}(x)\text{ which has no solution. Hence p3 has no turning points}\\\therefore\text{Using part (i) }p_{3}(x)\text{ has only one zero, in the interval [-25,0]}.$

Thought you only needed part iii anyway?

Also, I think you ment no real zero to p₂(x) or no real solution to p₂(x)=0

1008 · Apr 24, 2016

Yep, so I was just wondering how would InteGrand's explanation to part iii continue on from my working for the first two parts?

EDIT: Also, @leehuan, you're right, I mean there's no real solution to P2(x) = 0

InteGrand · Apr 24, 2016

1008 said:
Yep, so I was just wondering how would your explanation to part iii continue on from my working for the first two parts?

I used some stuff from your first two parts, like the fact that the second derivative is always positive.

1008 · Apr 24, 2016

Also, how would you do this one. I could only figure out one of the solutions.

$\\\text{Suppose that }a\geq0.\text{ Find the greatest and the least distances from the point }(a,0)\text{ to the ellipse}\\\frac{x^{2}}{4}+\frac{y^{2}}{1}=1$

Drsoccerball · Apr 25, 2016

1008 said:
Thanks! Here's another one:

$\\\text{The function } f \text{ is differentiable at }a\text{. Find:}\\\\\lim_{h \rightarrow 0}\frac{f(a+ph)-f(a-ph)}{h}$

lel hopitals <>

InteGrand · Apr 25, 2016

1008 said:
Also, how would you do this one. I could only figure out one of the solutions.

$\\\text{Suppose that }a\geq0.\text{ Find the greatest and the least distances from the point }(a,0)\text{ to the ellipse}\\\frac{x^{2}}{4}+\frac{y^{2}}{1}=1$

We can parameterise a point in the ellipse like x = t, y = sqrt(1 - (t^2/4)), for -2 <= t <= 2. (This only gets the top half of the ellipse but by symmetry, the distance will be same as considering the whole ellipse). We can then consider the squared distance of the point (a, 0) to a point on the ellipse (t, sqrt(1 - (t^2/4))), -2 <= t <= 2. We can then use calculus to minimise and maximise this. When we do the minimum, for some values of a, the answer is of a different shape than for other values of a. This is because for after some value of a, the actual point in the ellipse corresponding to the minimal distance with the other values of a would become a point with t having to be greater than 2, which means the point isn't on the ellipse (and the y-value would be imaginary). So a slightly different form of answer will be needed. The whole Q. is a bit tedious to write out now, so I've just given a method for now.

1008 · Apr 25, 2016

InteGrand said:
We can parameterise a point in the ellipse like x = t, y = sqrt(1 - (t^2/4)), for -2 <= t <= 2. (This only gets the top half of the ellipse but by symmetry, the distance will be same as considering the whole ellipse). We can then consider the squared distance of the point (a, 0) to a point on the ellipse (t, sqrt(1 - (t^2/4))), -2 <= t <= 2. We can then use calculus to minimise and maximise this. When we do the minimum, for some values of a, the answer is of a different shape than for other values of a. This is because for after some value of a, the actual point in the ellipse corresponding to the minimal distance with the other values of a would become a point with t having to be greater than 2, which means the point isn't on the ellipse (and the y-value would be imaginary). So a slightly different form of answer will be needed. The whole Q. is a bit tedious to write out now, so I've just given a method for now.

Thanks! Considering you gave a response at 3 in the morning!

But yeah, there are like 3 answers to the question. Here they are:
$\\\text{The greatest distance is }a+2;\text{ the least distance is } \begin{cases}\sqrt{1-\frac{a^{2}}{3}} & 0\leq{a}\leq{\frac{3}{2}}\\|a-2| & a > 3/2\end{cases}$ .

I could only get (1-a^2/3) by considering

1008 · Apr 25, 2016

Just another question:

$\\\text{Let f be continuous on [a,b]. Prove there exists c}\in(a,b)\text{ such that}\\\int_{a}^{b}f(t)\text{ }dt = f(c)(b-a).\\\\\text{The way I think I can do it:}\\\text{Consider the function }F(t)\text{ where }F'(t) = f(t)\\\text{As }f(t)\text{ is continuous on [a,b], }F(t)\text{ is differentiable on [a,b] and hence is also continuous.}\\\text{Hence we apply the Mean Value Theorem (MVT) over [a,b]}\\F'(c) =\frac{F(b) - F(a)}{b-a}, c\in(a,b)\\\text{As }F'(t) = f(t),\\f(c)(b-a) = F(b) - F(a).\text{ Now }F(b) - F(a) = \int_{a}^{b}f(t)\text{ }dt\\\therefore\int_{a}^{b}f(t)\text{ }dt=f(c)(b-a)$

Is this right, or am I missing something

InteGrand · Apr 25, 2016

1008 said:
Just another question:

$\\\text{Let f be continuous on [a,b]. Prove there exists c}\in(a,b)\text{ such that}\\\int_{a}^{b}f(t)\text{ }dt = f(c)(b-a).\\\\\text{The way I think I can do it:}\\\text{Consider the function }F(t)\text{ where }F'(t) = f(t)\\\text{As }f(t)\text{ is continuous on [a,b], }F(t)\text{ is differentiable on [a,b] and hence is also continuous.}\\\text{Hence we apply the Mean Value Theorem (MVT) over [a,b]}\\F'(c) =\frac{F(b) - F(a)}{b-a}, c\in(a,b)\\\text{As }F'(t) = f(t),\\f(c)(b-a) = F(b) - F(a).\text{ Now }F(b) - F(a) = \int_{a}^{b}f(t)\text{ }dt\\\therefore\int_{a}^{b}f(t)\text{ }dt=f(c)(b-a)$

Is this right, or am I missing something

That is indeed a valid method.

1008 · Apr 25, 2016

1008 said:
Also, how would you do this one. I could only figure out one of the solutions.

$\\\text{Suppose that }a\geq0.\text{ Find the greatest and the least distances from the point }(a,0)\text{ to the ellipse}\\\frac{x^{2}}{4}+\frac{y^{2}}{1}=1$

1008 said:
Thanks! Considering you gave a response at 3 in the morning!

But yeah, there are like 3 answers to the question. Here they are:
$\\\text{The greatest distance is }a+2;\text{ the least distance is } \begin{cases}\sqrt{1-\frac{a^{2}}{3}} & 0\leq{a}\leq{\frac{3}{2}}\\|a-2| & a > 3/2\end{cases}$ .

I could only get (1-a^2/3) by considering

Thanks! If you don't mind, could you also give a proof for this one InteGrand?

1008 · Apr 25, 2016

Drsoccerball said:
lel hopitals <>

Thanks! Why didn't I think of that?!

InteGrand · Apr 25, 2016

1008 said:
Thanks! If you don't mind, could you also give a proof for this one InteGrand?

So the ellipse condition is that the point P on the (upper-half of the) ellipse has $y = \sqrt{1-\frac{x^2}{4}}$ .

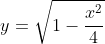
The squared distance as a function of x is then 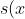$s(x) = (x-a)^2 + 1-\frac{x^2}{4}$ .

This can be differentiated to help find the minimum:

$s^\prime (x) = 2(x-a)-\frac{2x}{4}=2(x-a)-\frac{x}{2}=\frac{3}{2}x-2a$

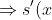$\Rightarrow s^\prime (x) = 0 \text{ when }\frac{3}{2}x-2a=0\Leftrightarrow x=\frac{4a}{3}$ .

So the minimal squared distance is $s_\text{min.}=\left(\frac{4a}{3} -a \right)^2 + 1 - \frac{\left(\frac{4a}{3} \right)^2}{4}=\frac{1}{3}(3-a)^2 = 1 - \frac{a^2}{3}$

From simplifying this, you get the top part of the answer you posted.

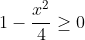
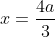
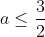
To see the reason for the split in answers for different values in a, note that $1-\frac{x^2}{4}\geq 0$ (since it's under a square root). Substituting $x=\frac{4a}{3}$ yields $a\leq \frac{3}{2}$ in order for the top half of the answer to be feasible. In other words, we need -2 ≤ x ≤ 2 for the point to be on the ellipse and make sense, but if a > 3/2, this no longer happens, as x becomes bigger than 2.

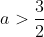
(For $a>\frac{3}{2}$ , the point on the ellipse we worked out as being closest, namely 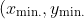$(x_\text{min.},y_\text{min.}) =\left(\frac{4a}{3},\sqrt{1-\frac{\left(\frac{4a}{3}\right)^2}{4}}\right)$ , is no longer a real point, which is why we need the condition on a.)

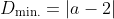
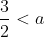
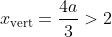
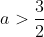
To see why using $D_\text{min.}=|a-2|$ when $\frac{3}{2}<a$ is optimal, note that the squared distance function represents a concave up parabola. Therefore, it is minimised at its vertex, and as we saw before, this globally minimising x-value is $x_\text{vert}=\frac{4a}{3}>2$ as $a>\frac{3}{2}$ . So the parabola is minimised at a point x_vert. where x_vert. > 2, so the closest we can get to this minimal value by taking a point on the ellipse (where x needs to be less than 2) is to make x closest to x_vert.. To make x closest to x_vert. and have x be on the ellipse, we need to take x = 2, as x_vert. > 2. 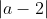This point (the point (2,0)) on the ellipse has distance to the point (a, 0) of $|a-2|$ as required.

(So basically I'm saying that if a quadratic is minimised at an x-value of x_vert., if we are restricted to x-values less than some maximal allowable value X, then the minimal attainable value for the quadratic is its value at this X (because the quadratic will be monotone decreasing on (-∞, X], as X < x_vert.). In our case, the maximal allowable value of X is X = 2 (this constraint coming from the ellipse). So taking x = 2 gives us the place of the min.)

Edit: Realised I didn't prove the maximal distance part. But this part is easier than the minimal part, so I'll leave it as an exercise for the reader.

Need help, URGENT maths question: (2 Viewers)

Well-Known Member

Well-Known Member

Active Member

Well-Known Member

Active Member

Active Member

Well-Known Member

Active Member

Well-Known Member

Active Member

Well-Known Member

Active Member

Well-Known Member

Well-Known Member

Active Member

Active Member

Well-Known Member

Active Member

Active Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 2)