Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon

From completion of the square, we require it to be strictly a sum of two positive squares.

From the modulus of the roots, we have:

Completing the square is more cumbersome so we resort to the discriminant.
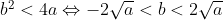
From the modulus of the roots, we have:
From completion of the square, we require it to be strictly a sum of two positive squares.
From the modulus of the roots, we have:
Completing the square is more cumbersome so we resort to the discriminant.
Last edited:
