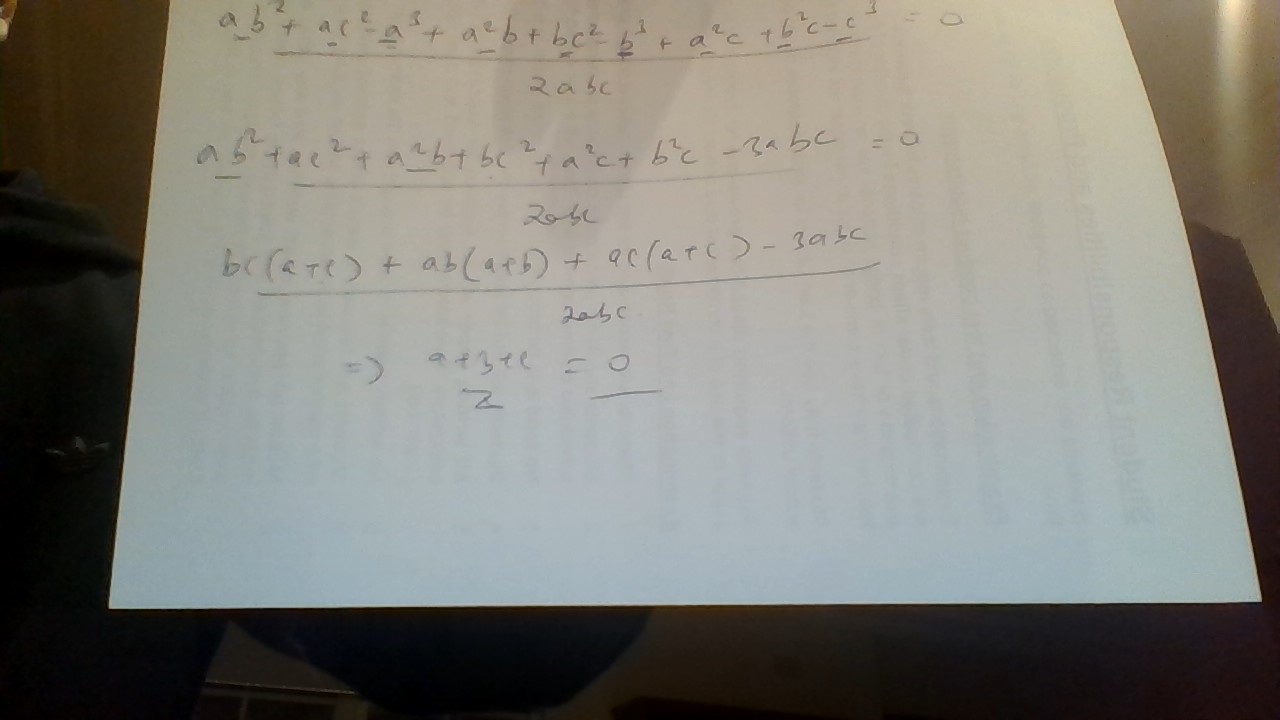Green Yoda
Hi Φ
- Joined
- Mar 28, 2015
- Messages
- 2,849
- Gender
- Male
- HSC
- 2017
If
a=cos(a)+sin(a)i
b=cos(b)+sin(b)i
c=cos(c)+sin(c)i
and a+b+c=0
Prove that 1/a + 1/b +1/c =0
a=cos(a)+sin(a)i
b=cos(b)+sin(b)i
c=cos(c)+sin(c)i
and a+b+c=0
Prove that 1/a + 1/b +1/c =0