Last edited:
-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2017-2018 Maths Marathon (2 Viewers)
- Thread starter dan964
- Start date
HoldingOn
Active Member
When you do working in 2u make sure to write out obvious statements, they may seem stupid but they are necessary to get the marks, particularly for curve sketching. For example above- include in your working a phrase like "testing nature," and a concluding statement "therefore horizontal point of inflexion at P(X,Y) etc.Im going to Year 10 in 2018 and am learning differential calculus, to answer OP's question I sketched the graph, any advanced criticism is appreciated as I am learning
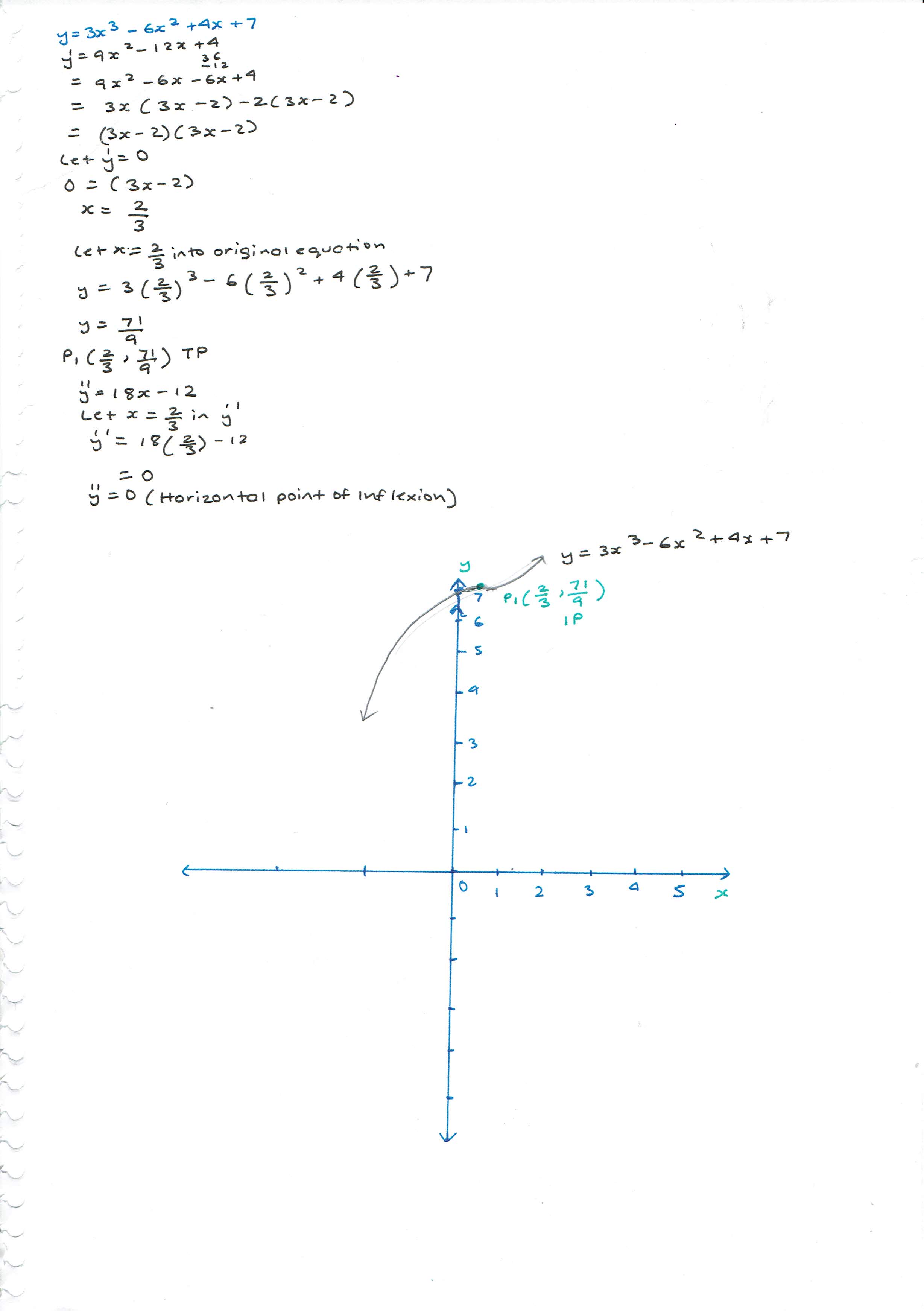
It doesn't matter if your graph's scale isn't perfect, you don't need to measure out centimetres on your ruler. As long as you sketch a reasonable graph, showing any necessary features (including any that were asked for) e.g. intercepts, maxima/minima, pts. of inflexion you'll get the marks. The intent is not to test you on your measuring skills.Im going to Year 10 in 2018 and am learning differential calculus, to answer OP's question I sketched the graph, any advanced criticism is appreciated as I am learning
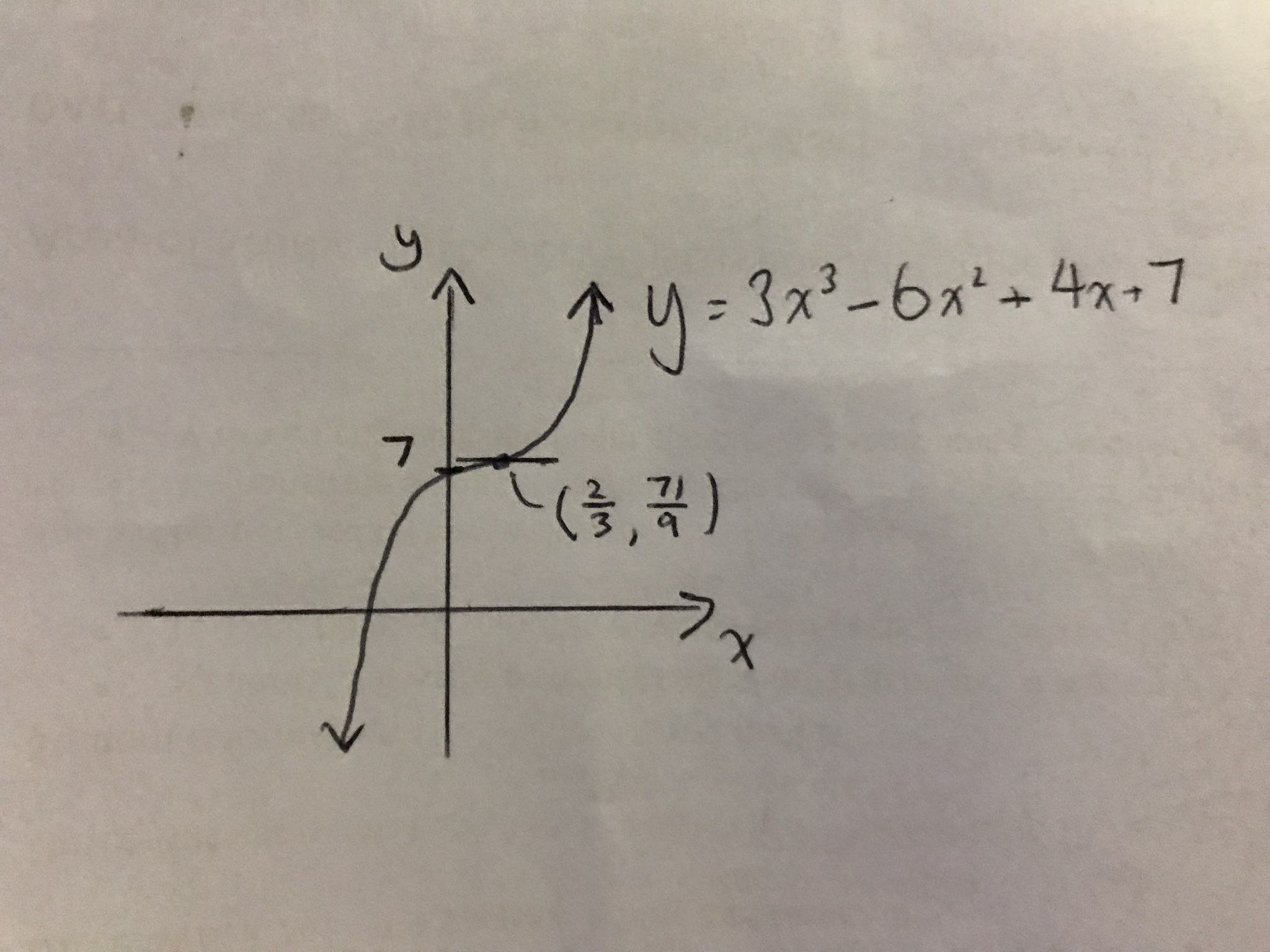
Just as a quick example, I would sketch it something like this. Just note that this graph shows the y-intercept more clearly. It's possible to find any x intercepts but this isn't expected in the 2U course, although it should be in the 3U course. I was taught to label my points of inflexion with a line going through the point but I don't think it matters as long as you make it clear that the point IS one of inflexion. In an exam I would draw the graph larger, though.
A point of inflexion means a change in concavity, i.e. from positive to negative or vice versa. so to prove that a point is one of inflexion, you need to show that the sign of the second derivative changes around that point.
for your curve:
Because
Just to elaborate on why you need to test the second derivative around the point - first note that any quadratic, such as
Consider the curve
Last edited:
pikachu975
Premium Member
Just a tiny tiny comment but make sure your horizontal point of inflection looks really horizontal so that if you drew a tangent to it the tangent would be horizontal.It doesn't matter if your graph's scale isn't perfect, you don't need to measure out centimetres on your ruler. As long as you sketch a reasonable graph, showing any necessary features (including any that were asked for) e.g. intercepts, maxima/minima, pts. of inflexion you'll get the marks. The intent is not to test you on your measuring skills.
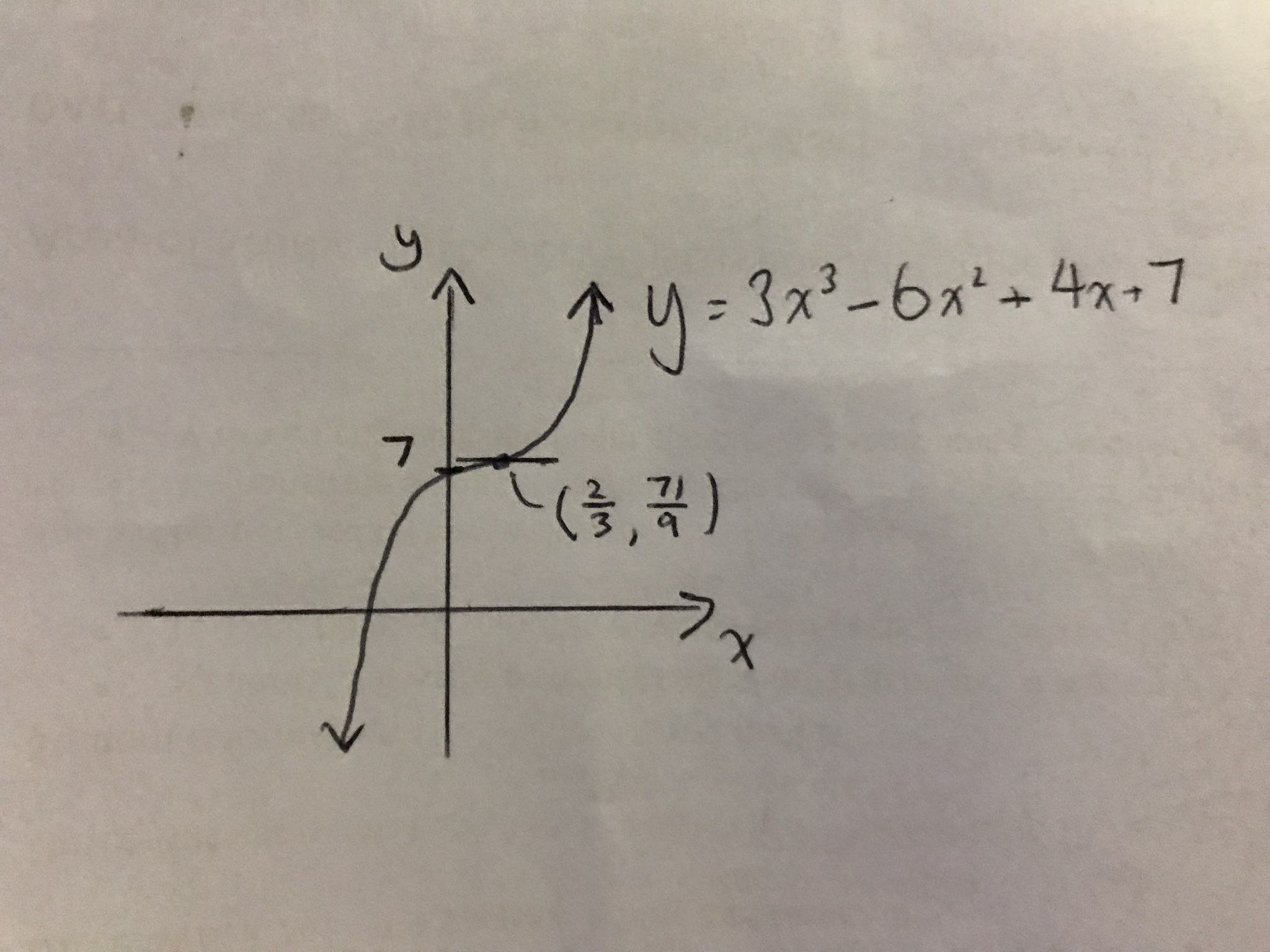
Just as a quick example, I would sketch it something like this. Just note that this graph shows the y-intercept more clearly. It's possible to find any x intercepts but this isn't expected in the 2U course, although it should be in the 3U course. I was taught to label my points of inflexion with a line going through the point but I don't think it matters as long as you make it clear that the point IS one of inflexion. In an exam I would draw the graph larger, though.
A point of inflexion means a change in concavity, i.e. from positive to negative or vice versa. so to prove that a point is one of inflexion, you need to show that the sign of the second derivative changes around that point.
for your curve:
Becausechanges signs around
, a point of inflexion exists at
.
Just to elaborate on why you need to test the second derivative around the point - first note that any quadratic, such as, has no points of inflexion because
is always a constant (in this case,
) and so the equation
has no solution.
Consider the curve. The curvature of the graph is identical to
(you can graph it digitally to check). Here,
, so the equation
has a solution at
. But from the previous paragraph, clearly this curve can't have a point of inflexion. This is because
for all real
, so the second derivative never changes signs and because of this, no points of inflexion exist on this curve.
HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
I asked my teacher he says about 3mm run in HPOI is goodJust a tiny tiny comment but make sure your horizontal point of inflection looks really horizontal so that if you drew a tangent to it the tangent would be horizontal.
Well in reality no one is gonna actually measure for 3mm run, around that should bbe fine

