HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
THis is from the 2015 perms thread
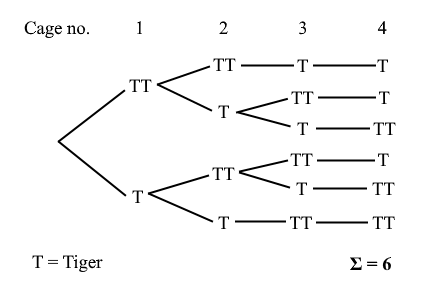
A zoo keeper wants to place 6 tigers in 4 cages, each can fit a maximum of two tigers.
In how many ways can he place the tigers if no cage to be left empty?
I got
4! x (6C2 x 4C2 x 2C1 x 1C1) = 4320
Because: First Cage: 6C2
Second Cage: 4C2
Third Cage: 2C1
Fourth Cage: 1C1
4! ways to arrange these
Some people got 2160 which is 4320/2
some also got 1080 which is 4320/4
IM confused to what is the right answer. If so why am I wrong
A zoo keeper wants to place 6 tigers in 4 cages, each can fit a maximum of two tigers.
In how many ways can he place the tigers if no cage to be left empty?
I got
4! x (6C2 x 4C2 x 2C1 x 1C1) = 4320
Because: First Cage: 6C2
Second Cage: 4C2
Third Cage: 2C1
Fourth Cage: 1C1
4! ways to arrange these
Some people got 2160 which is 4320/2
some also got 1080 which is 4320/4
IM confused to what is the right answer. If so why am I wrong