-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Optimisation Q (1 Viewer)
- Thread starter popjin
- Start date
Legend! That all makes sense now. Wish our textbooks had worked solutions like this.
\hspace{2mm}\text{(Trivial from here)})
Note that, for this optimisation, once you have the product  = 28x - x^2)
you can solve the problem without calculus. Plotting this function would give a concave-down parabola with roots at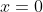 
and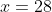 
and axis (and hence maxima) at the average of the roots (ie at 
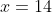) or from the formula 
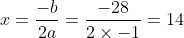. So, the numbers are 14 and 14 and the product is 196. Changing the values (to, say, 13 and 15) leads to the product (here 195) being smaller.
The n = 2 case of the AM-GM inequality states that, for any positive x and y, the arithmetic mean is greater than or equal to the geometric mean, and thus that:
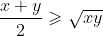
This can be easily proven by noting that, for any positive reals x and y, we can state with certainty that^2 \geqslant 0)
and then expanding.
Equality occurs only when x = y, which is also easily proven:
^2}{4} = xy \\ x^2 + 2xy + y^2 = 4xy \\ x^2 - 2xy + y^2 = 0 \\ (x - y)^2 = 0 \\ x - y = 0 \\ x = y)
Applying this to our problem, we have numbers x and y such that x + y = 28. As HeroWise has noted, we can thus conclude that:
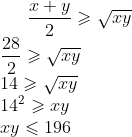
Since equality occurs when x = y, we know that the maximum product of 196 occurs when both numbers are 14. For any other pair of numbers that sum to 28 and to which the AM-GM inequality applies, we will get a product below 196, and so we have the solution.
There are two problems here, however:
1. Notice the caveat in my answer: to which the AM-GM inequality applies... The AM-GM inequality applies only if both numbers are positive and there is no such restriction in the question. This can be addressed by noting that:
* if one of x or y is negative then so must the product xy be negative (and thus less than 196), so this situation can't lead to a maximum value.
* if both are negative, their sum cannot possibly be 28.
So, we can eliminate all the cases where the AM-GM approach is invalid. However, in an exam, a marker might require that this be noted to give full credit to an AM-GM solution.
Note that both the calculus and graphing approaches described above do not have this problem as they allow for any solution in real numbers, and thus cover the same domain as was implied in the question.
2. In HeroWise's solution, the possibilty of x = 4 and y = 49 is considered as two other values that multiply to 196. It is important to recognise that HeroWise is making an assumption that the numbers must be integers, which is neither a requirement for the AM-GM inequality nor is it implied by the question. The question only implies that the two numbers are real. As I have noted above, we can conclude that they must also be positive, but this needs to be shown. It is dangerous to make assumptions when responding to questions / problems, and I urge all readers to recognise how easy it is to make an unjustified assumption and end up with an incorrect or (in this case) potentially incomplete solution.
PS: Is everyone getting "invalid equation" notices when using the tex tags at the moment? (Note: Equations edited)
This can be easily proven by noting that, for any positive reals x and y, we can state with certainty that
Equality occurs only when x = y, which is also easily proven:
Applying this to our problem, we have numbers x and y such that x + y = 28. As HeroWise has noted, we can thus conclude that:
Since equality occurs when x = y, we know that the maximum product of 196 occurs when both numbers are 14. For any other pair of numbers that sum to 28 and to which the AM-GM inequality applies, we will get a product below 196, and so we have the solution.
There are two problems here, however:
1. Notice the caveat in my answer: to which the AM-GM inequality applies... The AM-GM inequality applies only if both numbers are positive and there is no such restriction in the question. This can be addressed by noting that:
* if one of x or y is negative then so must the product xy be negative (and thus less than 196), so this situation can't lead to a maximum value.
* if both are negative, their sum cannot possibly be 28.
So, we can eliminate all the cases where the AM-GM approach is invalid. However, in an exam, a marker might require that this be noted to give full credit to an AM-GM solution.
Note that both the calculus and graphing approaches described above do not have this problem as they allow for any solution in real numbers, and thus cover the same domain as was implied in the question.
2. In HeroWise's solution, the possibilty of x = 4 and y = 49 is considered as two other values that multiply to 196. It is important to recognise that HeroWise is making an assumption that the numbers must be integers, which is neither a requirement for the AM-GM inequality nor is it implied by the question. The question only implies that the two numbers are real. As I have noted above, we can conclude that they must also be positive, but this needs to be shown. It is dangerous to make assumptions when responding to questions / problems, and I urge all readers to recognise how easy it is to make an unjustified assumption and end up with an incorrect or (in this case) potentially incomplete solution.
PS: Is everyone getting "invalid equation" notices when using the tex tags at the moment? (Note: Equations edited)
Last edited: