Theorem:
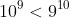
This sort of problem can be approached by calculus (as in the link provided by Drdusk), but calculus need not be used.
In this case, "proof" by calculator makes the result that
obviously true as
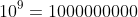
is one billion and
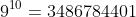
is over three billion. However, such an answer is not helpful in general as this type of response can be easily avoided by making the numbers larger. One alternative (and usable for larger numbers) is to re-write with a common base.
Proof 1 (common base):
We know from index laws that
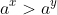
leads to the conclusion that
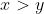
provided that the base a is real and
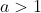
. So, if we can re-write
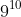
in the form
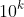
, the result is proved if
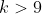
(or similarly, re-write
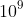
as
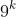
and show that
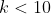
).
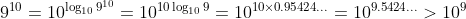
Or
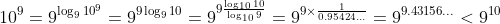
---
This proof is similar to a proof by caluclator, but it would allow you to prove that
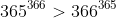
as
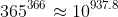
and
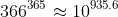
. The approach won't generalise to pronumerals, though, so looking at (say)
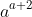
and
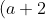^a)
for an appropriate domain of
a is not approachable in this way. (I note a suitable domain of a as
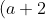^a)
is larger for
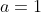
, the statements are equal for
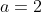
, and
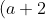^a)
is smaller for
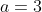
.

