Another approach is to look at the polynomial you seek to solve / factorise and separate the terms that can take on a odd value (restricting yourself to integers). Looking at the polynomial we have, every term will be even when x is an even integer, but when x is odd, there are only two terms that have an odd value, x4 and 19x2. So, we can say:
 = x^4 - 6x^3 - 19x^2 + 84x + 180 &= 0 \\ x^4 - 19x^2 &= 6x^3 - 84x - 180 \\ x^2(x^2 - 19) &= 6(x^3 - 14x - 30) \\ \cfrac{x^2(x^2 - 19)}{6} &= x^3 - 14x - 30 \end{align*})
I can see that any odd integer must give a value of) that is a multiple of 6, which allows for a quick search for odd integer solutions.
that is a multiple of 6, which allows for a quick search for odd integer solutions.
Case: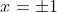
}{6} = \cfrac{(\pm1)^2\big((\pm1)^2 - 19\big)}{6} = \cfrac{1 \times -18}{6} = -3)
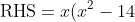 - 30 = x\big((\pm1)^2 - 14\big) - 30 = -13x - 30 < -3 \text{ for } x = \pm1)
So, neither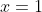 nor
nor 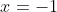 is a solution.
is a solution.
Case: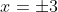
}{6} = \cfrac{(\pm3)^2\big((\pm3)^2 - 19\big)}{6} = \cfrac{9 \times -10}{6} = -15)
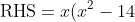 - 30 < -30 \text{ if } x = \pm3 > 0)
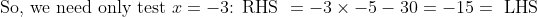
So, we have one solution,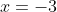 .
.
Case: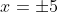
^2\big((\pm5)^2 - 19\big)}{6} = \cfrac{25 \times 6}{6} = 25)
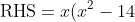 - 30 < 0 \text{ if } x = \pm5 < 0)
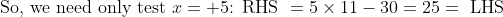
So, we have a second solution,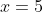 .
.
Having found two factors, we can divide) by
by (x + 3) = x^2 - 2x - 15) to find the second quadratic factor, which will be
to find the second quadratic factor, which will be 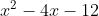 , but other approaches are faster.
, but other approaches are faster.
We know that we can take the rots to be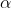 ,
, 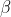 ,
, 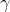 , and
, and 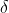 . We know two of these, so set
. We know two of these, so set 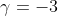 and
and 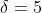 . We also know (from the constant being positive) that there are an even number of positive roots, and so one of the two roots we are yet to find is positive and the other is negative.
. We also know (from the constant being positive) that there are an even number of positive roots, and so one of the two roots we are yet to find is positive and the other is negative.
}{1} \implies \alpha + \beta = 4)
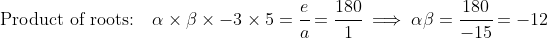
It immediately follows that the quadratic with roots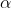 and
and 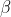 is
is x + \alpha\beta = x^2 - 4x - 12 = (x - 6)(x + 2)) which is also what the long division would find.
which is also what the long division would find.
Thus, we have:
 = x^4 - 6x^3 - 19x^2 + 84x - 180 = (x + 2)(x + 3)(x - 5)(x - 6))
and thus the solutions of = 0) are
are 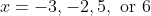 .
.
I can see that any odd integer must give a value of
Case:
So, neither
Case:
So, we have one solution,
Case:
So, we have a second solution,
Having found two factors, we can divide
We know that we can take the rots to be
It immediately follows that the quadratic with roots
Thus, we have:
and thus the solutions of
