Extending from my previous post and correcting an error...
We start with the proven result:
^n}{n!} \\ e^n n! &> (n + 1)^n \\ n! &> \frac{(n+ 1)^n}{e^n} \end{align*})
And use the substitution
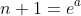
:
^n}{e^n} \\ &> \frac{(e^a)^n}{e^n} \\ &> e^{a \times n - n} \\ n! &> e^{n(a - 1)} \\ \ln n! &> n(a - 1) \text{ . . . . . . (1)} \end{align*})
Now, returning to the starting inequality, we had:
\ln (n + 1) - n < \ln (n + 1)!)
Applying the substitution
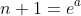
:
\ln (n + 1) - n < \ln (n+1)! \\ \ln n! &< e^a \ln e^a - n < \ln [(n+1) \times n!] \\ \ln n! &< ae^a - n < \ln e^a + \ln n! \\ \text{Yielding two results: } \ln n! &< ae^a - n \text{ . . . . . . (2A)} \\ \text{And} \ln n! &> ae^a - n - a \text{ . . . . . . (2B)} \end{align*})
Now, equations (1) and (2A) can be combined to conclude that
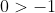
... which it true, but not terribly useful:
 \\ ae^a - n &> na - n \\ ae^a &> na \\ e^a &> n \\ e^a &> e^a - 1 \\ 0 &> -1 \end{align*})
The approach can be modified, however, increasing or decreasing one side of an inequality where the change cannot falsify the statement. This is akin to saying that if
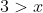
and that
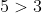
then I can say with certainty that
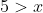
. In this case, I start by noting that
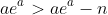
allows me to alter {2B):
 = (n + 1 - 1)a \\ &> (e^a - 1)a \\ ae^a &> ae^a - a \\ a &> 0 \end{align*})
Other variants include modifying (1A)'s term
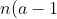)
like :
 \\ ae^a &> na - 2n + n = n(a - 1) \\ &> (e^a - 1)(a - 1) \\ ae^a &> ae^a - e^a - a + 1 \\ e^a &> 1 - a \end{align*})
(a - 1) \\ &> (e^a - 1 - 1)(a - 1) = (e^a - 2)(a - 1) \\ ae^a &> ae^a - 2a - e^a + 2 \\ 0 &> 2 - 2a - e^a \\ e^a &> 2 - 2a \end{align*})
These are getting closer, though the negative coefficient on the

is a problem. As an aside, we would be there if we can get
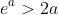
as this could be integrated from 0 to

to give
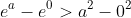
, which is the required result.
(a - 1) \\ 2ae^a &> 2(n - 1)(a - 1) + n = 2an - 2a - 2n + 2 + n = n(2a - 1) - 2a + 2 \\ &> (e^a - 1)(2a - 1) - 2a + 2 \\ 2ae^a &> 2ae^a - 2a - e^a + 1 - 2a + 2 \\ 0 &> 3 - 4a - e^a \\ e^a &> 3 - 4a \end{align*})
(a - 1) \\ ae^a &> an - a^2 - n + a - n = n(a - 2) - a^2 - a \\ &> = (e^a - 1)(a - 2) - a^2 - a \\ ae^a &> ae^a - a - 2e^a + 2 - a^2 - a \\ 0 &> 2 - 2a - a^2 - 2e^a \\ e^a &> \frac{2 - a - a^2}{2} \end{align*})
I don't see how this approach is going to yield any result
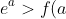)
where
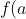)
has positive coefficients on any terms in

.

I've also been thinking about the geometric interpretations here:
- Consider the function
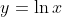 plotted from
plotted from 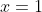 to
to 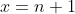 where
where 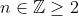 . Add divisions (for upper and lower rectangles) with width of 1 unit.
. Add divisions (for upper and lower rectangles) with width of 1 unit.
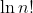 is the area of the resulting lower rectangles,
is the area of the resulting lower rectangles, !) are the upper rectangles, and so the inequality
are the upper rectangles, and so the inequality 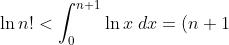\ln(n + 1) - n < \ln (n+1)!)
- Taking
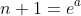 we have a rectangle with one side on the
we have a rectangle with one side on the  -axis covering
-axis covering 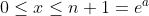 and one side on the
and one side on the 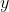 -axis covering
-axis covering 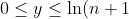 = a)
- The integral exists entirely within the rectangle, so that the area of the rectangle (
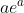 ) is divided into the part under the curve
) is divided into the part under the curve 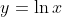 (with area
(with area 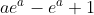 ) meaning the area above the curve (which is also the area under the curve against the
) meaning the area above the curve (which is also the area under the curve against the 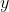 -axis has area
-axis has area 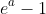
- This provides insight into some of the inequalities and the reason for the substitution, but does not yield a solution.
- I do wonder, though, if we need to work against the
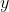 -axis and the diagonal for the large rectangle, and seek that the area against the
-axis and the diagonal for the large rectangle, and seek that the area against the 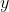 -axis to be greater than
-axis to be greater than 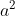 - but while still using the original result to satisfy the "hence" requirement.
- but while still using the original result to satisfy the "hence" requirement.
or
in which case the result
becomes
. We then need to bring in the integral result or some modification (I tried trapezoidal and it doesn't get us there) to get the final result.
has
for all
and
so
(and thus
) for all
.
