-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Vectors questions (1 Viewer)
- Thread starter R0L13D
- Start date
ratio division formula, nice respiration formula btw
R0L13D
New Member
- Joined
- Apr 3, 2020
- Messages
- 28
- Gender
- Male
- HSC
- 2021
can I see your working out please
just use ratio division formula and u get it. i ceebs rn to do working out lol.
@Qeru
chuck him latex.
Pretty sure cambridge has an example question that looks like this lol. u could look.
NOTE: This post has been edited to correct a significant mistake in my earlier reasoning.
The diagonals of a parallelogram bisect the angles only if the sides are equal in length, and thus only if it is a rhombus.
Thus, to bisect the angle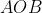
we need to adjust the vectors 
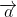and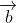 
to be unit vectors, and we can then say that the director of the angle bisector is the same as the direction of 
, the sum of the unit vectors. Then, since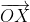 
is in this direction, it must be a scalar multiple of this vector and so )
.
Note: I am using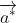
to mean the unit vector in the same direction as 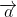, which I would handwrite as a vector with an under tilde and a hat, but the implementation of tex at BoS can't display that (as far as I know) because a package plug-in is required.
--- Part (b) ---
We know that
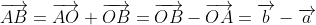
and
 \qquad \text{where $0 < \mu < 1$})
and
\left(\overrightarrow{b} - \overrightarrow{a}\right))
We seek to show that
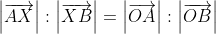
and the RHS of this
})
So, all you need to do now is to find
\right|}{\left|(1 - \mu)\left(\overrightarrow{b} - \overrightarrow{a}\right)\right|} \\ &= \frac{\mu\left|\overrightarrow{b} - \overrightarrow{a}\right|}{(1 - \mu)\left|\overrightarrow{b} - \overrightarrow{a}\right|} \\ &= \frac{\mu}{1 - \mu} \qquad \qquad \text{. . . . . . . . . (**)} \end{align*})
and show that it simplifies to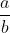
Now, we need to make use of the first part of the question in which we showed that. Recalling that the unit vector of any vector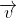 
is found by dividing by its magnitude, that is, that
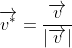
we have that
 = \lambda\left(\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|} + \frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\right) = \lambda\left(\frac{\overrightarrow{a}}{a} + \frac{\overrightarrow{b}}{b}\right) = \frac{\lambda}{a}\overrightarrow{a} + \frac{\lambda}{b}\overrightarrow{b})
We can also expres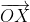s as
 = (1 - \mu)\overrightarrow{a} + \mu\overrightarrow{b})
Equating the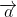 components of the two forms of 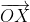gives
})
And, equating the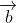 components of the two forms of 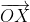gives
})
And thus
} \\ &= \mu \div (1 - \mu) \\ &= \frac{\lambda}{b} \div \frac{\lambda}{a} \qquad \qquad \text{using (1) and (2)} \\ &= \frac{\lambda}{b} \times \frac{a}{\lambda} \\ &= \frac{a}{b} \\ &= \frac{\left|\overrightarrow{OA}\right|}{\left|\overrightarrow{OB}\right|} \qquad \qquad \text{using (*)} \end{align*})
The diagonals of a parallelogram bisect the angles only if the sides are equal in length, and thus only if it is a rhombus.
Thus, to bisect the angle
Note: I am using
--- Part (b) ---
We know that
and
and
We seek to show that
and the RHS of this
So, all you need to do now is to find
and show that it simplifies to
Now, we need to make use of the first part of the question in which we showed that
we have that
We can also express
Equating the
And, equating the
And thus
Last edited:
For question 18
- Show that
- Show that
- Put these into
and expand / simplify to get
- Since this dot product is zero, you have part (a)
- From this result, you can show that
or
- Since you know the range of possible values for
, you can find the range of possible values for
- Note that one value is excluded as it allows only a single position for
Question 19 asks for a proof that the line
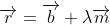where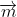 
is a unit vector
meets a sphere with centre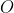
and radius 
at two points if
^2)
A line will touch a sphere if it is a tangent, and so if its perpendicular distance from the centre of the sphere is equal to the radius. The line will meet the sphere at two distinct points
and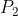 
if its perpendicular distance from the centre is less than the radius. So, the problem here is to find the condition for 
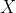, the closest point on the line to 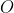and which lies somewhere on the interval 
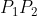, to be less than units from 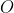. The shortest distance from a point to a line is the perpendicular distance, which in this case means that 
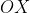is perpendicular to the line.
This could also be thought of by taking)
as any point on the line, letting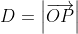 
be the distance between 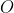and 
and seeking to show that the above condition corresponds to the minimum value of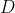 
, 
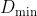, which occurs when is located at 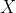, satisfies 
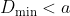. However, I don't think that a calculus-style max/min approach (here in 3 dimensions) is the way to approach the question - I mention it as a way to help visualise the problem.
In either case, I strongly suspect that the problem requires showing that
^2)
and I note that, since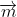 gives the direction of the line, we know that 
.
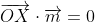Now, since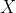 lies on the line, 
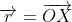satisfies the equation and so 
.
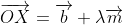 \cdot \overrightarrow{m} \\ 0 &= \overrightarrow{b} \cdot \overrightarrow{m} + \lambda\overrightarrow{m} \cdot \overrightarrow{m} \qquad \qquad \text{as $\overrightarrow{OX} \cdot \overrightarrow{m} = 0$} \\ 0 &= \overrightarrow{b} \cdot \overrightarrow{m} + \lambda\left|\overrightarrow{m}\right|^2 \\ 0 &= \overrightarrow{b} \cdot \overrightarrow{m} + \lambda \times 1 \qquad \qquad \text{as $\overrightarrow{m}$ is a unit vector and so $\left|\overrightarrow{m}\right| = 1$} \\ \lambda &= - \overrightarrow{b} \cdot \overrightarrow{m} \end{align*})
Thus, the position of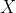, the closest point to 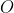on the line, corresponds to the point where 
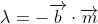and so
\overrightarrow{m})
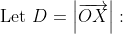
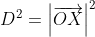
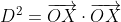
\overrightarrow{m}\right] \cdot \left[\overrightarrow{b} - \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)\overrightarrow{m}\right])
\overrightarrow{m} \cdot \overrightarrow{b} - \overrightarrow{b} \cdot \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)\overrightarrow{m} + \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)\overrightarrow{m} \cdot \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)\overrightarrow{m})
\left(\overrightarrow{b} \cdot \overrightarrow{m} + \overrightarrow{b} \cdot \overrightarrow{m}\right) + \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)^2\overrightarrow{m} \cdot \overrightarrow{m} \quad \text{as $\overrightarrow{b} \cdot \overrightarrow{m} = \overrightarrow{m} \cdot \overrightarrow{b}$})
^2 + \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)^2\left|\overrightarrow{m}\right|^2 \quad \text{as $\overrightarrow{m} \cdot \overrightarrow{m} = \left|\overrightarrow{m}\right|^2$})
^2 + \left(\overrightarrow{b} \cdot \overrightarrow{m}\right)^2 \quad \text{as $\left|\overrightarrow{m}\right| = 1$})
^2)
And we know that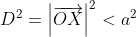
, and so
^2 < a^2)
as required.
meets a sphere with centre
A line will touch a sphere if it is a tangent, and so if its perpendicular distance from the centre of the sphere is equal to the radius. The line will meet the sphere at two distinct points
This could also be thought of by taking
In either case, I strongly suspect that the problem requires showing that
and I note that, since
Now, since
Thus, the position of
And we know that
as required.
R0L13D
New Member
- Joined
- Apr 3, 2020
- Messages
- 28
- Gender
- Male
- HSC
- 2021
Do you know which trial exams from what schools? also would u happen to have any resources for mx2 trials?For question 18
This question appeared on several MX2 trial exams in 2020.
- Show that
- Show that
- Put these into
- Since this dot product is zero, you have part (a)
- From this result, you can show that
- Since you know the range of possible values for
- Note that one value is excluded as it allows only a single position for
R0L13D
New Member
- Joined
- Apr 3, 2020
- Messages
- 28
- Gender
- Male
- HSC
- 2021
wait I'm confused as to why alpha cant equal pi/2For question 18
This question appeared on several MX2 trial exams in 2020.
- Show that
- Show that
- Put these into
- Since this dot product is zero, you have part (a)
- From this result, you can show that
- Since you know the range of possible values for
- Note that one value is excluded as it allows only a single position for
I saw it for the first time on an MX2 trial from a student of mine. I subsequently saw it on the paper from one of the companys that sells papers to schools for use on their trials.
I will post resources / questions here from time to time or when people ask a specific question. There are quite a few 2020 MX2 papers on THSC.
The question says that
Consider the diagram for the specific case that
It's not unusual for more challenging questions in Maths exams for there to be a difficult-to-get mark that requires some detail to be recognised and addressed.
As a simple example, suppose that solving
- getting to
could be worth 1 mark
- translating that to
or
could be the second mark
- recognising that
is excluded (as the original fraction was undefined) and thus the answer is
or
, could be the final mark
We are given that the coordinates of are )
and so
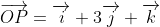
Now, if the point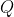
is represented by the position vector 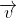, then we can say that 
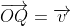. Since 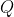is a point on the surface of the sphere with centre at , the radius must be the vector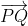 
:
 \end{align*})
And we know that the length of the radius is 14 units, so the sphere can be expressed in vector form as
\right| = 14)
Though it was not sought, we can find the Cartesian equation of the sphere by putting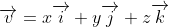
:
\right| &= 14 \\ \left|x\overrightarrow{i} + y\overrightarrow{j} + z\overrightarrow{k} - \left(\overrightarrow{i} + 3\overrightarrow{j} + \overrightarrow{k}\right)\right| &= 14 \\ \left|(x - 1)\overrightarrow{i} + (y - 3)\overrightarrow{j} + (z - 1)\overrightarrow{k}\right| &= 14 \\ (x-1)^2 + (y-3)^2 + (z-1)^2 &= 14^2 \end{align*})
Now, we know that)
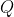is the point of contact of the tangent plane with the sphere. The vector for the radius at is
\overrightarrow{i} + (1 - 3)\overrightarrow{j} + (4 - 1)\overrightarrow{k} = \overrightarrow{i} - 2\overrightarrow{j} + 3\overrightarrow{k})
and the tangent plane is perpendicular to this vector.
Let)
be a point on the tangential plane, then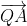 
is a vector in the plane given by
\overrightarrow{i} + (y - 1)\overrightarrow{j} + (z - 4)\overrightarrow{k})
As we now have a vector in the plane and a vector perpendicular to it, we know that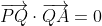
, which we can use to find the equation of the required plane:
 \cdot \left[(x - 2)\overrightarrow{i} + (y - 1)\overrightarrow{j} + (z - 4)\overrightarrow{k}\right] &= 0 \\ 1(x - 2) - 2(y - 1) + 3(z - 4) &= 0 \\ x - 2 + 2y + 2 + 3z - 12 &= 0 \\ x + 2y + 3z &= 12 \end{align*})
Now, if the point
And we know that the length of the radius is 14 units, so the sphere can be expressed in vector form as
Though it was not sought, we can find the Cartesian equation of the sphere by putting
Now, we know that
and the tangent plane is perpendicular to this vector.
Let
As we now have a vector in the plane and a vector perpendicular to it, we know that
R0L13D
New Member
- Joined
- Apr 3, 2020
- Messages
- 28
- Gender
- Male
- HSC
- 2021
HeY CM_Tutor. Just a question for Simple HArmonic Motion, how do u know what formula to use? Like for eg with this question:We are given that the coordinates of
Now, if the point
And we know that the length of the radius is 14 units, so the sphere can be expressed in vector form as
Though it was not sought, we can find the Cartesian equation of the sphere by putting
Now, we know that
and the tangent plane is perpendicular to this vector.
Let
As we now have a vector in the plane and a vector perpendicular to it, we know that
how would you know to use x = c - acosnt
and not x = c + asinnt
or x = c - a sinnt
or x = c + acosnt
or x = c + acos(nt + alpha)
why is it x = c - acosnt?
Hi ROL13D, the choice does not really matter in this case. The most general approach would be x = acos(nt + alpha) + c.
In this case I would use x = acosnt + c presuming you want time to be zero at 6:13AM. By making this choice a = -0.7, c = 1.2.
In the case of x = c - acosnt, then a = 0.7 and c = 1.2.
Assuming you want the coefficents to be positive for some weird reason then choice of x = c - acosnt will work. But it is not necessary and I personally would just stick with x = acos(nt + alpha) + c or x = c + acosnt (if you working maximum or minimum).
R0L13D
New Member
- Joined
- Apr 3, 2020
- Messages
- 28
- Gender
- Male
- HSC
- 2021
So the question of x doesn’t matter?
Yes, it will not matter for the most part.
Hi @R0L13D,
Any problem in SHM comes back to the second-order DE
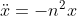
which has only one solution, but that can be written in a variety of equivalent forms, including:
 = A\sin(nt+\alpha) = B\sin{nt} + D\cos{nt})
The choice of which to use doesn't matter (in the sense that any will work) but does matter in that the choice can make the solutions more or less difficult. It is important to understand what each of the constants do:
)
by the substitution 
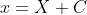or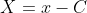 
. Historically, this was not considered sufficient to prove SHM, but I am unsure how it is seen after the syllabus change.
In any case, the key to SHM problems is to set up the problem so that:
Any problem in SHM comes back to the second-order DE
which has only one solution, but that can be written in a variety of equivalent forms, including:
The choice of which to use doesn't matter (in the sense that any will work) but does matter in that the choice can make the solutions more or less difficult. It is important to understand what each of the constants do:
- The
in the first two forms gives the amplitude of the motion as the trig function must be in
and so
. In the latter form, the amplitude is controlled by
and
- The
controls the period of motion, which is
- The
is a phase constant that translates the curve in time and should be zero if the problem is set up wisely.
In any case, the key to SHM problems is to set up the problem so that:
- The origin of position,
, is placed at the centre of the motion.
- The origin of time,
, is placed sensibly with respect to the motion. This means that it should be defined where the motion is either at its centre or at an extremity (maximum distance from the origin of position).
- In solving the DE, if the position at
- Following these, you should get
or
... in the latter case, the solution can be rewritten to eliminate
- Drawing a vertical axis, labelled
(for height above wharf) and mark on it
and
.
- Draw dashed horizontal lines across from these values, and also a SOLID LINE from the average (
).
- LEAVING A CENTIMETRE OR TWO SPACE TO THE RIGHT OF THIS
AXIS, I would draw a
curve between the
- I would now draw a vertical axis parallel to the
and
, with the minimum at
being at
and the position
.
- I can now add (in another colour) the time markings 6:13 am and 12:03 pm, the latter corresponding to
. I can also add the time for a complete cycle (at 5:53 pm or
) and the times at the centre of motion (9.08 am and 2:58 pm, half way in time between the extremities), if I so choose. This gives a feeling for when the required time will be, when the height above the wharf is 2.0 m.
- I would now write my definitions:
Let 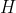be the height of the deck above the wharf at time 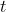hours after 6:13 am, so th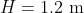at 
at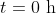 
.
Let be the difference between 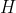and 1.9 m at time 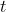, (i.e. 
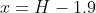) so that at , 
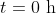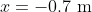
Now, since the motion is SHM about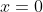
, we know that 
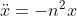, for some constant .
The solution of this DE is})
, for some constant and where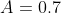 
.
At,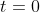 
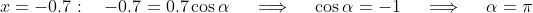
We know the period is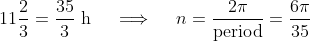
So,} = -0.7\cos{\left(\frac{6\pi t}{35}\right)})
We seek the times when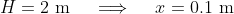
:
} \\ -\frac{1}{7} &= \cos{\left(\frac{6\pi t}{35}\right)} \\ \frac{6\pi t}{35} &= \pi - \cos^{-1}{\frac{1}{7}} &&\text{or} &&&\pi + \cos^{-1}{\frac{1}{7}} &&&&\text{or} &&&&&... \\ t &= \frac{35}{6\pi}\left(\pi - \cos^{-1}{\frac{1}{7}}\right) &&\text{or} &&&\frac{35}{6\pi}\left(\pi + \cos^{-1}{\frac{1}{7}}\right) &&&&\text{or} &&&&&... \\ &= 3.18283...\ \text{h} &&\text{or} &&&8.48383...\ \text{h} &&&&\text{or} &&&&&... \\ &= 3\ \text{h $10$ min $58.207...$ s} &&\text{or} &&&8\ \text{h $29$ min $1.792...$ s} &&&&\text{or} &&&&&... \end{align*})
So, the height of the deck above the wharf reaches 2.0 m at 3 h 11 min after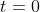, that is, at 9:24 am.
Though it is not asked, we see the deck returns to a height of 2.0 m above the wharf after 8 h 29 min, that is, at 2:42 pm.
We can use symmetry to recognise that this answer is correct as we know it took 2 h 39 min to reach its maximum height (at 12: 03 pm) from a height of 2.0 m, and will take the same amount of time to return to this height, and 2:42 pm is indeed 2 h 39 min after 12:03 pm.
Let
Now, since the motion is SHM about
The solution of this DE is
At
We know the period is
So,
We seek the times when
So, the height of the deck above the wharf reaches 2.0 m at 3 h 11 min after
Though it is not asked, we see the deck returns to a height of 2.0 m above the wharf after 8 h 29 min, that is, at 2:42 pm.
We can use symmetry to recognise that this answer is correct as we know it took 2 h 39 min to reach its maximum height (at 12: 03 pm) from a height of 2.0 m, and will take the same amount of time to return to this height, and 2:42 pm is indeed 2 h 39 min after 12:03 pm.
Attachments
Follow Up:
- If I chose to use a sine function, I would have
or
in my equations... though had I chosen
and would have found the solution
for the same result, a height of 2.0 m above the wharf at 9:24 am (nearest minute).
- If I chose to work in
.
- The biggest mistake you could make would be to set