Complex no. q (1 Viewer)

[=)(=]

 

[icycledough]

 

[Life'sHard]

View attachment 33398

Triangle inequality btw.

 

[=)(=]

View attachment 33399

how did you get the 2Re(zw) term?

 

[vishnay]

how did you get the 2Re(zw) term?

 

[icycledough]

If you add a complex number and its conjugate, as the complex portion of it cancels each other out, you're left with 2 x Re(zw).

So with a = 1 + i and b = 1 - i (which are conjugates), if you add them, you'll be left with 2, which is 2 x Re(a)

 

[5uckerberg]

how did you get the 2Re(zw) term?

Here is what is happening. Let's use a very simple term suppose , and there it becomes because the imaginary terms go into the trash since it is and both of these are zero.

 

[=)(=]

ohh makes so much sense now thanks a lot guys

 

[=)(=]

I am having troubling understanding this statement

 

[Life'sHard]

View attachment 33403
I am having troubling understanding this statement

This is pretty much vectors in complex no.s. You might find it a little difficult if you haven't yet learnt the basics of vectors assuming you're still in yr 10 lol.

 

[ExtremelyBoredUser]

View attachment 33403
I am having troubling understanding this statement

For purely real numbers, the argument is 0. (it can also be pi but to make it more apparent go with 0.)

Hence


through arg laws (kinda functions the same way as log laws do but you should know them by now)


Since there is two common points between both vectors being "A" or and the argument is the same for both vectors, all the points must be collinear.

If it still doesn't make sense, plot 3 random points labelling them and try drawing vectors that comply with the rule;

 

[Life'sHard]

For purely real numbers, the argument is 0. (it can also be pi but to make it more apparent go with 0.)

Hence


through arg laws (kinda functions the same way as log laws do but you should know them by now)


Since there is two common points between both vectors being "A" or "z_1" and the argument is the same for both vectors, all the points must be collinear.

You're learning latex

 

[=)(=]

For purely real numbers, the argument is 0. (it can also be pi but to make it more apparent go with 0.)

Hence


through arg laws (kinda functions the same way as log laws do but you should know them by now)


Since there is two common points between both vectors being "A" or and the argument is the same for both vectors, all the points must be collinear.

If it still doesn't make sense, plot 3 random points labelling them and try drawing vectors that comply with the rule;

ohhh that makes so much sense thx

 

[=)(=]

For the solution of part b I don't quite get the last step

 

[5uckerberg]

View attachment 33404
For the solution of part b I don't quite get the last step View attachment 33405

From part a we see that A, B and C are collinear. There we will see depending on the situation the three cases are what if and suppose we remove the absolute values and then consider the question at hand. We have from part a that so therefore we have where r is the distance and of course r will cancel becoming . There a diagram will look like the following

 

[5uckerberg]

Next step we will suppose that the right direction is positive so then what happens is that if then we see that C is to the left of A and as such going from A to C is t as shown by so now . The second case is where if t is between 0 and 1 which is 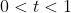and that as seen on the line is between A and B. We can see that and here, as we said once again but in this case where CB should be 1-t. The last case is where t > 1 and we see once again but this time C is further to the right than the distance AB so in this case we see that so therefore as such because we are getting different values for the different values of t. Due to the differences given by the distance AC, therefore, we need to find something that can explain the ratio of the distances with no dispute and as such noting the absolute values take into account of the opposite directions.

 

[=)(=]

thank you so much