Q23a)
Use your knowledge of vectors to complete this question noting that
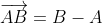
b)
Since we are focusing on the difference between the arguments between the real axis which we know for an Argand diagram is the x-axis. The angle is one minus the other angle since one line could be
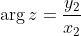
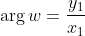
with the x-axis now we want the part between these two lines so, therefore, it becomes
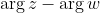
and the argument laws should finish the rest.
Q24)
Recall how vectors work. Slide w or z onto z or w respectively so using the parallelogram all will flow out naturally.
Q25a)
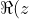)
is just the real section of the complex numbers which is x.
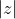
is the length of the complex number from the origin which gives us
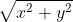
if you want them to be equal then make them the same.
b)
Starting with
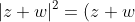\overline{(z+w)}=(z+w)(\bar{z}+\bar{w})=z\bar{z}+w\bar{w}+w\bar{z}+z\bar{w}=|z|^{2}+|w|^{2}+w\bar{z}+z\bar{w})
. Notice something here, do you recall what you said in Q25a if you can see that then it is clear that
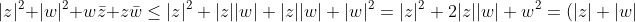^{2})
Therefore,
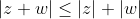
The infamous triangular inequality an mathematical phenomenom.
Anyways amdspotter is asking a lot of Qs from this chapter because he/she is finding difficulties with the exercises and wants some valuable guidance which we as members of Bored of Studies are keen to offer.