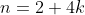For complex numbers, I get how we can solve for purely imaginary and/or purely real but letting sin or cos equal to zero. However, for some questions like the one below, the given set of k integers (for which a supposed n power makes the complex number zero or imaginary) is not always given by a set pattern. How would I approach and solve such questions?
View attachment 34497
Now prepare to witness the mind of a mathematician. The entire concept revolves around the fact that with a pattern where if we are finding something that is purely imaginary then for example we have
^{n}=0 )
which is simply
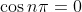
according to De Moivre's theorem.
The next step is just knowing the inverse of cosine when it's zero. This can be shown when
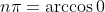
that is simply just
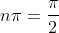
where
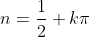
and many others that go in the cycle of
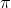
or
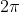
.
However, there is a variation of this type of question that asks us to find the smallest possible value of such an idea.
Consider the number
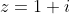
. Find the smallest value of

such that
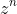
is purely imaginary. Then what is happening there is just simply to write this is polar form which is just length of
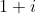
which is
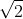
which is not too important here but might be important somewhere else such as finding mod-arg form, and then finding
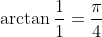
so thus, as such we have
}+i\sin{\left(\frac{n\pi}{4}\right)})
. Depending on what you want which is either purely real or imaginary convert either cosine or sine of the trig function to be zero and then find vaues which can be
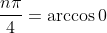
giving us
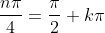
which then through simplification will give us