Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
How do I prove that functions increase? (1 Viewer)
- Thread starter jks22
- Start date
Thanks appreciate it! So if I prove it's always positive, can I say that a function is always increasing?Since the derivative isfor all real x, since square numbers are positive and
.
Therefore for all values of x within the domain ofwould be increasing.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Yes because once you have found the minimum turning point the function will only increase from the minimum turning point. If there is something lower than the minimum turning point you need to go back and check your calculations because there might be something lower.Thanks appreciate it! So if I prove it's always positive, can I say that a function is always increasing?
But for this specific question there is no minimum turning point, causeYes because once you have found the minimum turning point the function will only increase from the minimum turning point. If there is something lower than the minimum turning point you need to go back and check your calculations because there might be something lower.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Well, since 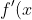 > 0 ) then the function is always increasing. Since you are doing Mathematics Advanced this concept will be a very useful one in the topic that many HSC candidates struggle with Cumulative Density Function found in the last chapter. Keep this question in your back pocket it may come in handy.
then the function is always increasing. Since you are doing Mathematics Advanced this concept will be a very useful one in the topic that many HSC candidates struggle with Cumulative Density Function found in the last chapter. Keep this question in your back pocket it may come in handy.
