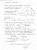-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
ineq q (1 Viewer)
- Thread starter =)(=
- Start date
Bob99
temporarylol hater
- Joined
- Apr 1, 2022
- Messages
- 228
- Gender
- Male
- HSC
- 2022
i dont do 4u, but ig expand it and then somehow simplify it lolView attachment 36087
kinda lost
Lol thanks but it’s something to do with am gm but I can’t see what it isi dont do 4u, but ig expand it and then somehow simplify it lol
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Have a look at this solution.View attachment 36087
kinda lost
Attachments
-
1.4 MB Views: 46
Ohhh i see it now thanksHave a look at this solution.
wizzkids
Well-Known Member
- Joined
- Jul 13, 2016
- Messages
- 389
- Gender
- Undisclosed
- HSC
- 1998
I remember a classic geometric proof of this inequality. I like this proof because it is easy to grasp, and elegant. As a couple of others have said, it is closely related to the arithmetic mean/geometric mean inequality.
I also offer a second, more conventional, algebraic proof that relies on the property of square numbers.
See the attached image files.
I also offer a second, more conventional, algebraic proof that relies on the property of square numbers.
See the attached image files.
Attachments
-
373.8 KB Views: 21
-
190.6 KB Views: 18
Last edited:
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,100
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
Damn that is so clean.I remember a classic geometric proof of this inequality. I like this proof because it is easy to grasp, and elegant. As a couple of others have said, it is closely related to the arithmetic mean/geometric mean inequality. See the attached image file.
chilli 412
oo la la
- Joined
- Apr 13, 2022
- Messages
- 249
- Gender
- Male
- HSC
- 2023
that was very elegant and easy to understandI remember a classic geometric proof of this inequality. I like this proof because it is easy to grasp, and elegant. As a couple of others have said, it is closely related to the arithmetic mean/geometric mean inequality. See the attached image file.