gamja
Active Member
- Joined
- Dec 14, 2022
- Messages
- 116
- Gender
- Undisclosed
- HSC
- 2023
Q5b of the above hsc paper:
- The graphs of y=f(x) [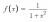 for x>=0] and y=invf(x) [which I calculated to be
for x>=0] and y=invf(x) [which I calculated to be 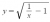 ]meet at exactly one point P. Let α be the x-coordinate of P. Explain why α is a root of the equation
]meet at exactly one point P. Let α be the x-coordinate of P. Explain why α is a root of the equation
x^3 +x -1 = 0.
I let both function formulae equal each other and squared them and eventually came out with a long 5-th degree polynomial. Any ideas? (much appreciated 
- The graphs of y=f(x) [
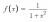 for x>=0] and y=invf(x) [which I calculated to be
for x>=0] and y=invf(x) [which I calculated to be 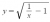 ]meet at exactly one point P. Let α be the x-coordinate of P. Explain why α is a root of the equation
]meet at exactly one point P. Let α be the x-coordinate of P. Explain why α is a root of the equationx^3 +x -1 = 0.
