Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
complex number euler form modulus question (1 Viewer)
- Thread starter gamja
- Start date
yanujw
Well-Known Member
- Joined
- May 23, 2020
- Messages
- 338
- Gender
- Male
- HSC
- 2022
The most prominent method is to let 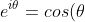 + isin(\theta)) . Then use the fact that
. Then use the fact that 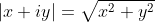
The locus of z itself is an ellipse which would have been helpful in the old syllabus. However, there is still a geometric way to find the maximum value.
Recall that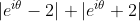 means the combined distance of
means the combined distance of 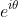 from the points 2 and -2 on the Argand diagram. And
from the points 2 and -2 on the Argand diagram. And 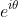 represents the unit circle of points. The combined length of the two vectors as visualised below is maximised* at either the points i or -i (see diagram below). At these points, each line has a length of
represents the unit circle of points. The combined length of the two vectors as visualised below is maximised* at either the points i or -i (see diagram below). At these points, each line has a length of 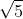 so the maximum combined length is
so the maximum combined length is 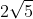
*this is just a vague conclusion based on looking at the graph, it may require an actual proof which just goes back to the algebraic version anyways.
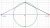
The locus of z itself is an ellipse which would have been helpful in the old syllabus. However, there is still a geometric way to find the maximum value.
Recall that
*this is just a vague conclusion based on looking at the graph, it may require an actual proof which just goes back to the algebraic version anyways.

Last edited:
The geometric method (see your diagram) is the easiest to understand and the shortest.The most prominent method is to let. Then use the fact that
The locus of z itself is an ellipse which would have been helpful in the old syllabus. However, there is still a geometric way to find the maximum value.
Recall thatmeans the combined distance of
from the points 2 and -2 on the Argand diagram. And
represents the unit circle of points. The combined length of the two vectors as visualised below is maximised* at either the points i or -i (see diagram below). At these points, each line has a length of
so the maximum combined length is
*this is just a vague conclusion based on looking at the graph, it may require an actual proof which just goes back to the algebraic version anyways.
View attachment 37914
member 6003
Member
- Joined
- Apr 20, 2022
- Messages
- 85
- Gender
- Male
- HSC
- 2023
I was the dude, cool solution but ofc its outside the syllabus. I saw 2sqrt(5) in my solution so I just thought it would be correct without considering any logic before posting.Some dude (can't remember who) came here before and tried to use the AM-GM inequality to do it but it didn't work. They kind of had a good idea but had the inequality the wrong way around.
However the AM-QM inequality does work (instead of the AM-GM one):
^2+\sin^2\theta+(\cos\theta+2)^2+\sin^2\theta}{2}}\\&=2\sqrt{\frac{\cos^2\theta+\sin^2\theta-4\cos\theta+4+\cos^2\theta+\sin^2\theta+4\cos\theta+4}{2}}\\&=2\sqrt{\frac{10}{2}}\\&=2\sqrt5\text{ with equality }\iff|e^{i\theta}-2|=|e^{i\theta}+2|\iff\cos\theta=0\iff\theta=\frac{(2k+1)\pi}{2}\forall k\in\Bbb Z\end{aligned})
member 6003
Member
- Joined
- Apr 20, 2022
- Messages
- 85
- Gender
- Male
- HSC
- 2023
well if you prove first then yea they couldn't mark you down for it
