Take
a and
b as unit vectors from the origin (
O), representing points
A and
B on the unit circle. The angle between the vectors is
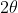
. Since the distance
AB is the length of the vector
a -
b and it is less than one, the isosceles triangle
AOB must have the radii as its longest sides, meaning the angle
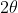
is no more than 60 degrees. Hence, the solution should be:
)
Unfortunately, this isn't provided as an option. However, since

, the length of vector
a -
b shortens again as
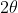
exceeds pi, and so there is another set of solutions for


