eternallyboreduser
Well-Known Member
- Joined
- Jul 4, 2023
- Messages
- 549
- Gender
- Undisclosed
- HSC
- N/A
How to do?
y=cos2x can be rewritten as 2cos^2 x -1How to do?
but what if you were in an exam and couldnt use desmos to geaoh lol, wouldbt ur geaph br much more inaccurate so its a bit hatder to telly=cos2x can be rewritten as 2cos^2 x -1
mx-1=2cos^2x -1
mx=2cos^2x
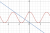
if u sketch this you get something like this (desmos isn't required since you just need a rough idea of what to look for)
View attachment 42089
you can observe that when m is between some values, the line is above the curve of 2cos^2x
from this you can probably just use pythagoras' theorem to figure out the bounds for m
edit:nvm pythag might be bad and lead to bad things just use calculus and figure out when y=mx is tangent
nah it doesn't rly matter you just gotta get a rough idea of what you're looking forbut what if you were in an exam and couldnt use desmos to geaoh lol, wouldbt ur geaph br much more inaccurate so its a bit hatder to tell
not exactly in the mood currently to do step by step but the rough idea should be differentiating it and plugging it into slope form, maybe sure that the y intercept is 0i havent done calculus with trig yet but do u mind providinf a dteo by step w/o @WeiWeiMan
how would u figure out the exact x value the tangent is atnah it doesn't rly matter you just gotta get a rough idea of what you're looking for
if you wanna find the shape of the graph just sub in some points into your calculator and use the fact that the thing is an even function
not exactly in the mood currently to do step by step but the rough idea should be differentiating it and plugging it into slope form, maybe sure that the y intercept is 0
calculus with trig shouldn't that that much different from calculus with anytyhing else
also i could be mistaken and my method could be completely wrong so please don't hold this against me
idk if this would be the best approach, observing mx=2cos^2x is harder to graph as opposed to mx-1=cos2xy=cos2x can be rewritten as 2cos^2 x -1
mx-1=2cos^2x -1
mx=2cos^2x
if u sketch this you get something like this (desmos isn't required since you just need a rough idea of what to look for)
View attachment 42089
you can observe that when m is between some values, the line is above the curve of 2cos^2x
from this you can probably just use pythagoras' theorem to figure out the bounds for m
edit:nvm pythag might be bad and lead to bad things just use calculus and figure out when y=mx is tangent
bro do yk how to do rhe qidk if this would be the best approach, observing mx=2cos^2x is harder to graph as opposed to mx-1=cos2x
calculus ig idkhow would u figure out the exact x value the tangent is at
do yk how to solveforget what I just said that was dumb asf
Yeah idk atp. I feel like just answering generally using the graph is the only real method.do yk how to solve
thats kinda hard to do during exam though cos ur geaph most definitely aint gonna be 100% accurateYeah idk atp. I feel like just answering generally using the graph is the only real method.
it doesn't ahve to be u just need a general idea of what ur looking forthats kinda hard to do during exam though cos ur geaph most definitely aint gonna be 100% accurate
may i ask how you're expected to find these valuesI would work with the equations as given.
There will be one solution whenis large, so there will be two sets of possible values,
and
where the value
correspond to the line being a tangent to the curve at some value
and the line also crossing the curve at some point between
and
.
The values are aboutand
.
but then how r u gonna find the x valueit doesn't ahve to be u just need a general idea of what ur looking for
may i ask how you're expected to find these values
also i'm not sure but i feel like the question might want some exact bounds
u dont. ur finding values for m. x is a fnctionbut then how r u gonna find the x value
yeah but when u diff cos2x wouldnt u sub in a x value where the two functions touch each other once (aka the x value where y=x-1 is a tangent)u dont. ur finding values for m. x is a fnction
