Integral question (1 Viewer)

kendricklamarlover101 · Jan 25, 2024

can someone check if my working is correct i got this integral from spivak's calculus
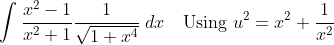
$\int \frac{x^2 -1}{x^2 +1} \frac{1}{\sqrt{1+x^4}} \; dx \quad \text{Using } u^2 = x^2 + \frac{1}{x^2}$
$u^2 = x^2 + \frac{1}{x^2} \implies 2u \; du = \left(2x - \frac{2}{x^3}\right)dx$
$u \; du = \left(x - \frac{1}{x^3}\right)dx$
$= \frac{x^4-1}{x^3} \; dx = \frac{(x^2-1)(x^2+1)}{x^3} \; dx$
$\implies dx = \frac{ux^3 \; du}{(x^2-1)(x^2+1)}$
$\int \frac{x^2 -1}{x^2 +1} \frac{1}{\sqrt{1+x^4}} \; dx = \int \frac{x^2 -1}{x^2 +1} \frac{1}{x\sqrt{x^2 + \frac{1}{x^2}}} \; dx$
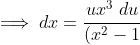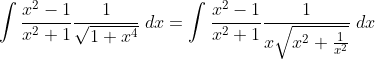
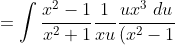$=\int \frac{x^2 - 1}{x^2 + 1} \frac{1}{xu} \frac{ux^3 \; du}{(x^2-1)(x^2+1)} = \int \frac{x^2}{\left(x^2 +1\right)^2} \; du$
$=\int \frac{x^2}{x^2 \left( x +\frac{1}{x} \right)^2} \; du = \int \frac{1}{u^2 + 2} \; du$
$=\frac{1}{\sqrt{2}} \arctan \left( \frac{u}{\sqrt{2}} \right) = \frac{1}{\sqrt{2}} \arctan \left( \frac{\sqrt{x^4+1}}{x\sqrt{2}} \right) + C$
also are there any alternative methods than this substitution?

Drongoski · Jan 25, 2024

I've checked. Seems to be correct. Congratulations.
I would not expect you to have Michael Spivak's textbook.

kendricklamarlover101 · Jan 25, 2024

yea my tutor gave me the textbook cause he thought i would have liked some of the questions. at first i tried using a trig substitution but i couldnt get anywhere with that so i was just wondering if there was another solution.

Drongoski · Jan 25, 2024

kendricklamarlover101 said:
yea my tutor gave me the textbook cause he thought i would have liked some of the questions. at first i tried using a trig substitution but i couldnt get anywhere with that so i was just wondering if there was another solution.

You've done very well to do the integration with the suggested substitution. I tried x^2 = tan@ - fruitless.

kendricklamarlover101 · May 29, 2024

i recently found another way to do this integral and thought it was pretty cool
$\int \frac{x^2 - 1}{x^2+1}\frac{dx}{\sqrt{1+x^4}} = \int \frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}}\frac{dx}{\sqrt{x^2\left(x^2+\frac{1}{x^2}\right)}}$
$=\int \frac{ 1 - \frac{1}{x^2} }{\left( x + \frac{1}{x} \right) \left( \sqrt{x^2 + \frac{1}{x^2} } \right)}dx = \int \frac{ 1 - \frac{1}{x^2} }{\left( x + \frac{1}{x} \right) \left( \sqrt{\left(x+\frac{1}{x}\right)^2-2} \right)}dx$
$\text{Let } u=x+\frac{1}{x}, \; du = \left(1 - \frac{1}{x^2}\right)dx$
$I= \int\frac{du}{u\sqrt{u^2-2}}$
$\text{Let } u=\sqrt{2}\sec \theta, \; du=\sqrt{2}\sec\theta\tan\theta d\theta$
$I= \int\frac{\sqrt{2}\sec\theta\tan\theta d\theta }{\sqrt{2}\sec\theta\sqrt{2\sec^2\theta - 2} } =\int\frac{\sqrt{2}\sec\theta\tan\theta d\theta }{\sqrt{2}\sec\theta\sqrt{2}\tan\theta}$
$= \frac{1}{\sqrt{2}}\sec^{-1}\left(\frac{x+\frac{1}{x}}{\sqrt{2}}\right) + C$

imagineee · May 29, 2024

Yep that's the way I would've done it, although the trig sub is kind of unnecessary since you can change I to 1/u^2(1-2/u^2)^1/2 then it's essentially reverse chain-ruleable into a standard arcsine/arccos integral

Integral question (1 Viewer)

kendricklamarlover101

Member

Drongoski

Well-Known Member

kendricklamarlover101

Member

Drongoski

Well-Known Member

kendricklamarlover101

Member

imagineee

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)