-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
more proof (1 Viewer)
- Thread starter Sylfiphy
- Start date
liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,102
- Gender
- Female
- HSC
- 2023
ideally you should use the sin angle sum formula, that is sin(a+b) = sinacosb+sinbcosa.prove: sin3x-sinx = 2sinx-4sin³x
here's what I have so far:
LHS = 2cos3x+x/2 sin 3x-x/2
= 2cos2xsinx
RHS= 2sinx-4sin³x
= 2sinxcos2x
so LHS=RHS
but its wrong and idk why🥲
then lhs = sin3x-sinx= sin(2x+x)-sinx = sin2xcosx+sinxcos2x-sinx
=2sinxcos^2x+sinx(1-2sin^2x)-sinx from double angle formulas
= 2sinx(1-sin^2x)-2sin^3x from pythagorean identity
=2sinx-4sin^3x=RHS
Average Boreduser
Rising Renewal
continue on w ur lhs. ur literally like 1 step away dudprove: sin3x-sinx = 2sinx-4sin³x
here's what I have so far:
LHS = 2cos3x+x/2 sin 3x-x/2
= 2cos2xsinx
RHS= 2sinx-4sin³x
= 2sinxcos2x
so LHS=RHS
but its wrong and idk why🥲
Average Boreduser
Rising Renewal
spoiler alertideally you should use the sin angle sum formula, that is sin(a+b) = sinacosb+sinbcosa.
then lhs = sin3x-sinx= sin(2x+x)-sinx = sin2xcosx+sinxcos2x-sinx
=2sinxcos^2x+sinx(1-2sin^2x)-sinx from double angle formulas
= 2sinx(1-sin^2x)-2sin^3x from pythagorean identity
=2sinx-4sin^3x=RHS
Average Boreduser
Rising Renewal
lhs= 2cos2xsinxprove: sin3x-sinx = 2sinx-4sin³x
here's what I have so far:
LHS = 2cos3x+x/2 sin 3x-x/2
= 2cos2xsinx
RHS= 2sinx-4sin³x
= 2sinxcos2x
so LHS=RHS
but its wrong and idk why🥲
expand ur cos2x,
lhs= 2(1-2sin^2x)*sinx
continue on from there.
Sylfiphy
Active Member
- Joined
- Feb 5, 2024
- Messages
- 109
- Gender
- Male
- HSC
- 2025
I always realise after someone humbles me but appreciate it yocontinue on w ur lhs. ur literally like 1 step away dud
Sylfiphy
Active Member
- Joined
- Feb 5, 2024
- Messages
- 109
- Gender
- Male
- HSC
- 2025
thank uuuuuuideally you should use the sin angle sum formula, that is sin(a+b) = sinacosb+sinbcosa.
then lhs = sin3x-sinx= sin(2x+x)-sinx = sin2xcosx+sinxcos2x-sinx
=2sinxcos^2x+sinx(1-2sin^2x)-sinx from double angle formulas
= 2sinx(1-sin^2x)-2sin^3x from pythagorean identity
=2sinx-4sin^3x=RHS
This thread actually illustrates how identity problems allow for multiple solutions, some quicker than others:
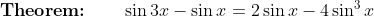
Proof 1: Conventional LHS / RHS approach
} - \sin{x} \\ &= \sin{2x}\cos{x} + \cos{2x}\sin{x} - \sin{x} \\ &= 2\sin{x}\cos{x} \times \cos{x} + \left(1 - 2\sin^2{x}\right)\sin{x} - \sin{x} \qquad \text{using the double angle formulae} \\ &= \sin{x}\left(2\cos^2{x} + 1 - 2\sin^2{x} - 1\right) \\ &= \sin{x}\left[2\left(1 - \sin^2{x}\right) - 2\sin^2{x}\right] \qquad \text{using the Pythagorean identity $\sin^2{\theta} + \cos^2{\theta} = 1$} \\ &= \sin{x}\left(2 - 2\sin^2{x} - 2\sin^2{x}\right) \\ &= 2\sin{x} - 4\sin^3{x} \\ &= \text{RHS} \end{align*})
Proof 2: LHS / RHS approach making use of a sums-to-products formula
 \qquad \text{using the double angle formula $\cos{2\theta} = 1 - 2\sin^2{\theta}$} \\ &= 2\sin{x} - 4\sin^3{x} \\ &= \text{RHS} \end{align*})
Proof 3: Direct Proof without LHS / RHS
} &= \sin{2x}\cos{x} + \cos{2x}\sin{x} \\ &= 2\sin{x}\cos^2{x} + \left(\cos^2{x} - \sin^2{x}\right)\sin{x} \qquad \text{using the double angle formulae} \\ &= 3\sin{x}\cos^2{x} - \sin^3{x} \\ &= 3\sin{x}\left(1 - \sin^2{x}\right) - \sin^3{x} \qquad \text{using the Pythagorean identity $\sin^2{\theta} + \cos^2{\theta} = 1$} \\ \text{Thus,} \qquad \sin{3x} &= 3\sin{x} - 4\sin^3{x} \\ \\ \text{Hence,} \qquad \sin{3x} - \sin{x} &= 2\sin{x} - 4\sin^3{x} \qquad \text{as required} \end{align*})
Proof 1: Conventional LHS / RHS approach
Proof 3: Direct Proof without LHS / RHS

