tickboom
Member
- Joined
- Aug 21, 2020
- Messages
- 72
- Gender
- Male
- HSC
- 2001
- Uni Grad
- 2008
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
From (i) expand the x^n and (1+ 1/x)^n into each other:Hi all, I'm a bit stuck on part ii) of this question. Part i) was easy enough, and I also know how to prove part ii) using Pascal's identity. But I can't see the link between part i) and part ii), which seems to be implied by the word "hence" in the question. Any ideas?
View attachment 29657
Legendary. Thank you!From (i) expand the x^n and (1+ 1/x)^n into each other:
Equate the x^r terms from the RHS and the LHS.
For the LHS we get
Equating the coefficients to the x^r term of the RHS which iswe get the solution
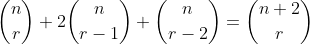
No video recording of your working? Kinda disappointing...From (i) expand the x^n and (1+ 1/x)^n into each other:
Equate the x^r terms from the RHS and the LHS.
For the LHS we get
Equating the coefficients to the x^r term of the RHS which iswe get the solution
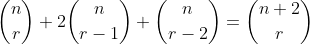
You could also expandHi all, I'm a bit stuck on part ii) of this question. Part i) was easy enough, and I also know how to prove part ii) using Pascal's identity. But I can't see the link between part i) and part ii), which seems to be implied by the word "hence" in the question. Any ideas?
View attachment 29657
