Re: Australian Maths Competition 2013
OK. I remembered two questions:
Given positive integer
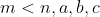
and
=0,f(n)=2016^2)
where
=ax^2+bx+c)
. How many values of
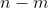
?
How many pairs (a,b) of positive integers such that
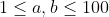
and
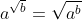
.
Well the first one is fairly simple in terms of the first step.
(a(n+m)+b)(n-m) = 2016² = 3⁴×7²×2¹⁰
n-m must be a perfect square so that means we should pull out all the possible square factors from the factorisation of 2016²
There's also the special case where the factors are equal.
If I'm reading that correctly, I'm seeing that m must also be less than all the integer coefficients of the quadratic, which is going to be a huge road block for people who like to bash problems.
The second one requires cases
a
√b = a
b/2
There are two ways this equation can be true.
1. The exponents are equal, so √b = b/2
=> b=4, a can be anything in the valid range.
2. a=1, therefore b can be anything in the valid range.
Observe the case a=1, b=4 is double counted, so subtract one from the final amount of solutions.
I think that's all, though I may be missing something glaringly obvious.

