Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
sketch y = x^1/2 (1 - x)
And Hence sketch a graph of the function y^2 = x(1 - x)^2
The domain of
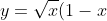 )
is
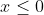
The intercepts are at x=0 and x=1
Expanding and then differentiating, the derivative function is
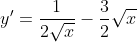
(And kind of unnecessary here, but
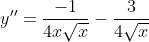
)
The stationary points are found by letting y'=0 as this is when the tangent to the curve is horizontal. Solving y'=0 you get x= 1/3 (and so

Using the first derivative test you will find that to the left of x=1/3 the derivative is positive (so increasing curve) and to the right the derivative is negative (so decreasing curve), meaning you have a maximum turning point. (Also, as this is the only turning point and there are no asymptotes etc. you know it is also the 'global' maximum). In addition, as y' is undefined at x=0, a point at which y exists, we have a vertical tangent at x=0.
Letting y''=0 for possible inflexion points we get x=-1/3 but that is not in our domain so it can be disregarded. We therefore can say the curve is concave down because we already know we have a maximum turning point and that the curve cannot change in concavity.
We can then draw the curve.
Also to draw the y^2=... function we can square root both sides. that brings us to the
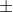
version of the original curve. So we simply draw the curve we just drew and then draw the 'flip' of it around the x-axis... but we KEEP BOTH CURVES.



