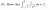Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
 + c$, for some arbitrary constant $c$ (remember to evaluate the antiderivative at the endpoints to get the value of the definite integral).$)
View attachment 32782
Having trouble with part b
Using part a), I took the integral of both side and I got this
Integral of tan^-1 x dx = xtan^-1 x - Integral of x/(1 + x^2) dx
So I need to find the integral of x/(1 + x^2)
Is this the correct method??