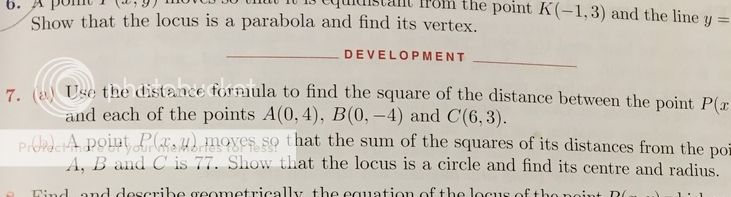pikachu975
Premium Member
Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
You didn't give us point A B and CQ 7 (b) EX 9A
I just wondering has there been a mistake in this answer of the 3U Year 11 textbook?
^2 )
^2 + (y + 4)^2 and )
ii) ==> PA² + PB² + PC² = 3x² + 3y² - 14x - 6y + 78 = 77
==> 3x² + 3y² - 14x - 6y = -1
==> x² + y² - 14x/3 - 2y = -1/3
Grouping, (x² - 14x/3) + (y² - 2y) = -1/3
==> (x² - 14x/3 + 49/9) + (y² - 2y + 1) = -1/3 + 49/9 + 1
==> (x - 7/3)² + (y - 1)² = 55/9
^2 + (y - k)^2 = r^2, $ )

The back of the book has the answer as (2,1) for centre and radius of