ekjchale#1
Active Member
- Joined
- Apr 4, 2022
- Messages
- 118
- Gender
- Male
- HSC
- 2022
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
I never heard of sin^-1 being defined for complex numbers. CoolConsidering this is a range question we need to focus on the domain between [-1, 1] because otherwise, we will have complex numbers for both which will require complex analysis which is way too out of your reach.
Here, forat x=-1, 0, 1 you will see that they have the following values
.
So therefore,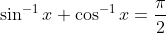
I am talking about something like this. For example,I never heard of sin^-1 being defined for complex numbers. Cool
Ah fair I tried that but it seemed way to simple lol, thanks for the clarification @5uckerberg @cossine @Run hard@thehscIf the derivative is zero this means the function is constant. So once you plug in some point that is in the domain you will get the answer.
So if you have y = sin^-1(x) + cos^-1(x)Ah fair I tried that but it seemed way to simple lol, thanks for the clarification @5uckerberg @cossine @Run hard@thehsc
Ah yep that makes senseSo if you have y = sin^-1(x) + cos^-1(x)
Then dy/dx = 0. So you have a differential equation that you can solve. Another alternative would be draw triangles.
So draw triangle with hypotenuse 1 and opposite side x for sin^-1(x) and hypotenuse 1 and adjacent side x for cos^-1(x). You will see the two angles will need to add up to 90.

