The question is

Letting (θ+ pi) = ɸ
I found the gradient of the chord, then the equation of it, cleaned it up but ended up getting
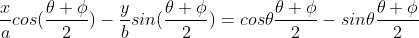
giving
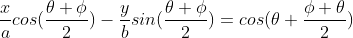
but as ɸ = (θ+ pi)
the RHS is then
 whereas i think it should be
whereas i think it should be 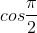
I don't know what i did wrong or what i'm meant to do next
Edit : This 4U Cambridge 3.2 Q3 btw
Letting (θ+ pi) = ɸ
I found the gradient of the chord, then the equation of it, cleaned it up but ended up getting
giving
but as ɸ = (θ+ pi)
the RHS is then
I don't know what i did wrong or what i'm meant to do next
Edit : This 4U Cambridge 3.2 Q3 btw
Last edited:
