-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
(Circ Motion) Why does using a vector diagram and the centripetal acceleration formula give different values? (1 Viewer)
- Thread starter erucibon
- Start date
Can you give an example?Why does using a vector diagram and the centripetal acceleration formula give different values? (using exact values in both so it isn't rounding errors)
One possible reason may be that the formula you're using has implicit assumptions (e.g. uniform circular motion).
I think it might be because your doing the operations incorrectly. For example you can't just add or subtract two vectors the same way as numbers like 2+3. You need to consider what direction they're pointing and work out the resultant vectors magnitude appropriately using Pythagorus and what not.Can you give an example?
One possible reason may be that the formula you're using has implicit assumptions (e.g. uniform circular motion).
Regardless an example would suffice for us to clear this up.
A mass lies on a perfectly smooth horizontal surface and is connected to a 1.2m string. The mass completes 5 rotations per second. Position B differs from Position A by 60 degrees.
Calculating the acceleration using the centripetal acceleration formula with 5 rotations per second as the speed gives 1184ms-2. By calculating the time it takes to move to B (0.033s, exact value is used in acceleration calculation), and then drawing a vector diagram to find change in velocity and then finding acceleration through change in velocity over time, I get 1131ms-2 (using exact values).
^2}{1.2} )
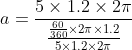
Shouldn't the magnitude of centripetal acceleration be the same regardless of whether it is moving from one point to another?
Calculating the acceleration using the centripetal acceleration formula with 5 rotations per second as the speed gives 1184ms-2. By calculating the time it takes to move to B (0.033s, exact value is used in acceleration calculation), and then drawing a vector diagram to find change in velocity and then finding acceleration through change in velocity over time, I get 1131ms-2 (using exact values).
Shouldn't the magnitude of centripetal acceleration be the same regardless of whether it is moving from one point to another?
Your second acceleration formula doesn't actually give the correct instantaneous acceleration - rather, an approximation of it.
Consider a more extreme case:
After the mass leaves point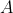 , it will again return to
, it will again return to 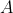 (after
(after  seconds have passed).
seconds have passed).
The vector for change in velocity here is, of course, the zero vector (with magnitude zero).
This implies the acceleration is zero.
Now this is completely true (depending on what is meant by acceleration), but it's not the answer we want.
Why? Because this method only considers two points - the start and the end. The path of the mass was never taken into account.
Between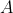 and
and  , the mass may as well have gone to the moon and back - as long as its initial and final velocities didn't change, we'd have no way of telling.
, the mass may as well have gone to the moon and back - as long as its initial and final velocities didn't change, we'd have no way of telling.
That's not to say that the second method is useless. With a bit of basic calculus, you can add a restriction of (uniform) circular motion and derive the centripetal force formula from it.
Consider a more extreme case:
After the mass leaves point
The vector for change in velocity here is, of course, the zero vector (with magnitude zero).
This implies the acceleration is zero.
Now this is completely true (depending on what is meant by acceleration), but it's not the answer we want.
Why? Because this method only considers two points - the start and the end. The path of the mass was never taken into account.
Between
That's not to say that the second method is useless. With a bit of basic calculus, you can add a restriction of (uniform) circular motion and derive the centripetal force formula from it.
Last edited:
Sydney Learning Hub
New Member
- Joined
- Jan 26, 2020
- Messages
- 2
- Gender
- Male
- HSC
- N/A
Hi,
vector diagram: averages out the acceleration of the object between 2 points while
centripetal acceleration formula: finds the instantaneous acceleration.
The difference lies in using differentiation (the formula) versus the small change in values (the diagram).
Then again, when drawing the diagram you are not drawing the acceleration but the final velocity and the initial velocity to find the change in values.
Regards
Sydney Learning Hub
sydneylearninghub.com
We provide tutoring services for year 11 and year 12 HSC Physics and Chemistry.
vector diagram: averages out the acceleration of the object between 2 points while
centripetal acceleration formula: finds the instantaneous acceleration.
The difference lies in using differentiation (the formula) versus the small change in values (the diagram).
Then again, when drawing the diagram you are not drawing the acceleration but the final velocity and the initial velocity to find the change in values.
Regards
Sydney Learning Hub
sydneylearninghub.com
We provide tutoring services for year 11 and year 12 HSC Physics and Chemistry.

