2.
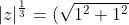^{\frac13}=\sqrt[6]{2})
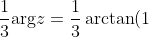=\frac\pi{12})
So the "primary root" will be
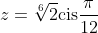
3. Note that 1/3arg(z) can also take other values namely:
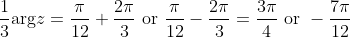
So other roots will be:
)
4. Convert cis roots to cartesian which will be quite laborious in this instance because the arguments aren't nice so compound/double angle formulae for cos and sin will be required.