Same idea as akshat but another way is: Let
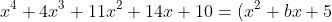(x^2+cx+2))
(5 and 2 since constant terms multiply to 10). Now compare coefficients of x^3 and x to get
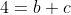
and
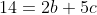
solving these simultaneous equations:
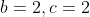
So
=(x^2+2x+5)(x^2+2x+2))
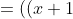^2+4)((x+1)^2+1))
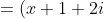(x+1-2i)(x+1+i)(x+1-i))
. The solutions are clear from here.
How do you know that your constant terms have to be 2 and 5? I agree they must multiply to give 10, but a complete solution would need to explain the exclusion of 1 and 10. And, what about -2 and -5 and the like? There is a good reason why these can be excluded, but would you know it or include it?
---
A similar approach is to recognise that, since the roots come in conjugate pairs (which we also know as the coefficients of the quartic are real), then there must be quadratic factors of the form:
(x-\bar{\alpha}) = x^2 - (\alpha + \bar{\alpha})x + \alpha\bar{\alpha} = x^2 - 2\Re{(\alpha)}x + |\alpha|^2)
Using the given roots
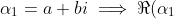} = a \text{ and } |\alpha_1|^2 = a^2 + b^2)
and
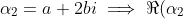} = a \text{ and } |\alpha_2|^2 = a^2 + 4b^2)
gives that our quartic factorises as
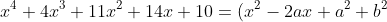(x^2-2ax+a^2+4b^2))
and thus, by equating coefficients for
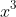
gives
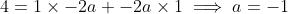
and by equating coefficients for
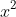
, we get:
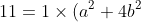 + -2a \times -2a + (a^2 + b^2) \times 1 = 6a^2 + 5b^2)
which, on using
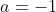
, becomes:
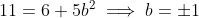
From this:
- the factorisation over
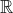 is:
is: 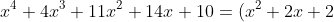(x^2+2x+5))
- the solutions of
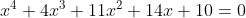 are:
are: 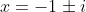 and
and 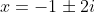
- the factorisation over
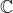 is:
is: 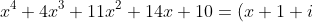(x+1-i)(x+1+2i)(x+1-2i))
Note that Qeru's completing-the-square method for finding the roots from the factorisation over
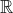
is useful to remember as an approach in complex numbers:
(x^2+2x+2) \\ &= \left[(x^2 + 2x + 1) + 4\right]\left[(x^2 + 2x + 1) + 1\right] \\ &= \left[(x + 1)^2 + 4\right]\left[(x + 1)^2 + 1\right] \\ &= \left[(x + 1)^2 - (2i)^2\right]\left[(x + 1)^2 - i^2\right] \\ &= (x + 1 + 2i)(x + 1 - 2i)(x + 1 + i)(x + 1 - i) \end{align*})

