mr.habibbi
Member
- Joined
- Oct 27, 2019
- Messages
- 41
- Gender
- Male
- HSC
- 2021
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
typoi^3 is -i
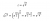
if you find the solution to the complex root, you get a plus minus (±) result, so you can take out or add a minus to (1-i) to get (-1+i) and still get the same result? hence C and D should work rightActually, D is -1 x C.
C has negative real part and a positive imaginary part whereas D has a positive real part and a negative imaginary part.
so if we were asked to find the solutions toNo, it is not.has a single value.
Firstly, I was showing that the values (C) and (D) are different.so if we were asked to find the solutions towe wouldn't put the plus minus?
Trebla is absolutely correct. The issue has to with symbols. The actual square root sign/symbolif you find the solution to the complex root, you get a plus minus (±) result, so you can take out or add a minus to (1-i) to get (-1+i) and still get the same result? hence C and D should work right
After line 2 you could argue that you need to change need to convertNo, it is not.has a single value.
i think this q has occurred more than once lol. not too sure though.After line 2 you could argue that you need to change need to convertto be in the range
aka
So that when you take the squareroot, the result is in the principal argument rangeto ensure that the real value of the solution > 0.
So D is justified and is technically more correct. Although I would mark C and D as both correct as it is ambiguous. Which paper was this from (as I might correct it)
Very well put. One of the main motivations for defining the principal value Arg is to be able to write complex numbers in modulus-argument form. Hence for any complex number z,I have read the posts from @Trebla and @dan964 carefully. I believe that we are all in agreement that:
To be completely honest, neither the definition that the principal square root must have a positive real part nor that it must have an argument that is an element of
- both (C),
, and (D),
, are solutions of
- (C) and (D) are different complex numbers
- there is an ambiguity created by the use of the square root symbol for te same reason that
has two solutions of which
is only one.
is a decimal approximation to the expression for the square root of two, while we would all recognise that
is not... but extending the convention to which is the "positive" square root of a complex number is a matter of definition.
strike me as definitive on first look. However, I have come to the conclusion that both are natural consequences of the definition that does make sense to me. Consequently, I withdraw my earlier statement that (C) is the best answer and agree that Dan and Trebla are correct that (D) is the most technically correct answer.
My reasoning reaches their conclusion from a slightly different route, which is that the principal square root of a complex number in mod-arg form is the square root taken on the complex number expressed that is itself expressed with its principal argument. Thus:
The flaw in my earlier reasoning was that, in expressing
as
, I did not restrict it to being expressed with its principal argument before taking the square root; rather, I only considered whether the result had a principal argument. Restricting the complex number to its principal argument before taking the square root has the consequences that the restrictions suggested by Trebla and Dan must be satisfied.
Thank you, and I agree. Once I realised that I was not using the principal argument in expressingVery well put. One of the main motivations for defining the principal value Arg is to be able to write complex numbers in modulus-argument form. Hence for any complex number z,
So by definition when using Euler's rule or De Moivre's we have to convert our results in be in that interval.
cranbrook 2020 4u trialsThank you, and I agree. Once I realised that I was not using the principal argument in expressing, and that doing so would necessarily lead to the conditions that you and @Trebla described, I saw that you had to be correct. Thank you to you both for helping me to see where I was mistaken.
I do hope someone identifies the source of the question so that you can consider adding a note on THSC.
