Refer to the last question of the Terry Lee vectors exercise for a purely algebraic answer.
Can someone start me off, because I've got no clue what to do, but not finish it. I wanna have a go.
Also need help with the last question of my paper, and then I'm done!!! I've tried employing the strategies you guys showed me in the previous questions, but this one puts me off because there are 3 brackets, and the vectors are reversed.
z1,z2,z3 are represented by the points p1,p2,p3 respectively. If p1p2p3 is an equilateral triangle, show
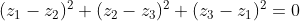
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Complex (1 Viewer)
- Thread starter nrlwinner
- Start date
I can't seem to se how the last line proves they're collinear.Well, I don't know how to draw a diagram here, so I'll have to describe it for you.
Draw your circle through O, predominantly in the first quadrant. Let A, B, C represent z1, z2, z3 respectively. For ease of describing, draw O, A, B, C in clockwise order (and in left to right order), all in the first quadrant. (The same logic works if they are drawn otherwise.) Produce AB to D.
Angle AOC = arg z1 - arg z3.
Angle CBD = arg (z1 - z2) - arg (z2 - z3)
(Tell me if you don't get that)
So arg (z1 - z2) - arg (z2 - z3) = arg z1 - arg z2 [ext angle of cyclic quad = opp int angle]
Rearrange:
arg(z1 - z2) - arg z1 = arg (z2 - z3) - arg z3
Add in the same 'fudge factor' on both sides of the =:
arg (z1 - z2) - arg z1 - arg z2 = arg (z2 - z3) - arg z3 - arg z2
Can you see that it is now proved?
- Joined
- Feb 16, 2005
- Messages
- 8,613
- Gender
- Male
- HSC
- 2006
If you think about it in vector terms, if the arguments are equal they are at least parallel. However, since the complex number 1/z2 is common in both equalities then the vectors must have a common point as well as be parallel which implies they must be collinear.
Thanks.I got it now.
Also.
For the polynomial z^4 -2z^3 +7z^2 -4z +10,
find real values of a for which ai is a solution.
I know it has something to do with conjugate root theorem, but I'm not sure how to apply it without actual numbers.
Also.
For the polynomial z^4 -2z^3 +7z^2 -4z +10,
find real values of a for which ai is a solution.
I know it has something to do with conjugate root theorem, but I'm not sure how to apply it without actual numbers.
Let P(x)=z^4-2z^3+7z^2-4z+10Thanks.I got it now.
Also.
For the polynomial z^4 -2z^3 +7z^2 -4z +10,
find real values of a for which ai is a solution.
I know it has something to do with conjugate root theorem, but I'm not sure how to apply it without actual numbers.
P(ai)=a^4+2a^3.i+7a^2-4ai+10
P(-ai)=a^4-2a^3+7a^2+4ai+10
P(ai)+P(-ai)=2(a^4-7a^2+10)=0
(a^2-5)(a^2-2)=0
a=+-sqrt(5) and +-sqrt(2)
Let A,B,C,D be roots of P(z):
A+B+C+D=2
C+D=2 and CD=5 or 2
C^2+D^2=(C+D)^2-2CD
ie. C^2+D^2=-6 or 0 but we know C=/=+-iD as this would not satisfy poly equ
Thus, CD=5
C^2-2C+5=0
(C-1)^2=-4
C=1+2i, D=1-2i
Thus, z=+-sqrt(2)i or 1+-2i
ie a=+-sqrt(2)
Last edited:
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
alternatively
=z^4 -2z^3 +7z^2 -4z +10\\$If $ai $ is a root of $P(z), $ then $ P(ai)=0=0+0i\\P(ai)=(ai)^4-2(ai)^3+7(ai)^2-4(ai)+10=(a^4-7a^2+10)+i(2a^3-4a)=0+0i\\$Equating $\Re(P(ai)),\\a^4-7a^2+10=(a^2-5)(a^2-2)=0\Rightarrow a=\pm \sqrt{5},\pm \sqrt{2}\\$Equating \Im(P(ai)),\\2a^3-4a=2a(a^2-2)=0, \text{ where } a\neq \pm \sqrt{5}\\a=\pm \sqrt{2} \text{ is the common solution and thus }a=\pm \sqrt{2})
Last edited:
Nice, a lot better than my solution but i think i could've just cut-off a=+-sqrt(5) before hand as a solutionalternatively
=z^4 -2z^3 +7z^2 -4z +10\\$If $ai $ is a root of $P(z), $ then $ P(ai)=0=0+0i\\P(ai)=(ai)^4-2(ai)^3+7(ai)^2-4(ai)+10=(a^4-7a^2+10)+i(2a^3-4a)=0+0i\\$Equating $\Re(P(ai)),\\a^4-7a^2+10=(a^2-5)(a^2-2)=0\Rightarrow a=\pm \sqrt{5},\pm \sqrt{2}\\$Equating \Im(P(ai)),\\2a^3-4a=2a(a^2-2)=0, \text{ where } a\neq \pm \sqrt{5}\\a=\pm \sqrt{2} \text{ is the common solution and thus }a=\pm \sqrt{2})
I need help on this question.
I did the first part and got |z|=2 as a locus
But what is the locus of w where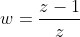
K
khorne
Guest
Algebraically:
a^2 + b^2 = 4
w = a+ib - 1 / a+ib, after simplifying:
w = 4-a+ib/4
w = x+iy, so equate:
x = 4-a/4 and y = b/4
a^2 = 16(x-1)^2
b^2 = 16y^2
resub:
16(x-1)^2 + 16y^2 = 4
(x-1)^2 + y^2 = 1/4
|w-1| = 1/2
a^2 + b^2 = 4
w = a+ib - 1 / a+ib, after simplifying:
w = 4-a+ib/4
w = x+iy, so equate:
x = 4-a/4 and y = b/4
a^2 = 16(x-1)^2
b^2 = 16y^2
resub:
16(x-1)^2 + 16y^2 = 4
(x-1)^2 + y^2 = 1/4
|w-1| = 1/2
ninetypercent
ninety ninety ninety
if w + w^4 and w^2 + w^3 are roots of the equation, then
sum of roots = w + w^4 + w^2 + w^3 = -1
product of roots = (w + w^4)(w^2 + w^3) = w^3 + w^6 + w^4 + w^7 = w^3 + w^4 + w + w^2 = -1
the equation is
z^2 - (sum of roots) z + product of roots = 0
z^2 + z -1 = 0
which is the equation given in question
sum of roots = w + w^4 + w^2 + w^3 = -1
product of roots = (w + w^4)(w^2 + w^3) = w^3 + w^6 + w^4 + w^7 = w^3 + w^4 + w + w^2 = -1
the equation is
z^2 - (sum of roots) z + product of roots = 0
z^2 + z -1 = 0
which is the equation given in question
K
khorne
Guest
What are you doing up at 11pm doing 4U?
ninetypercent
ninety ninety ninety
^ he might have tutor hw or something due.
I know this sound so simple, but I've never had to find the roots (apart for square) for something in cartesian form. I've always done it either just as a real number of just as an imaginary number.
Find the five-fifth roots of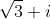
and I'm tryna finish all my complex work tonight and I've got like 5 questions out of 153 I can't do
Find the five-fifth roots of
and I'm tryna finish all my complex work tonight and I've got like 5 questions out of 153 I can't do
ninetypercent
ninety ninety ninety
the trick is to convert sqrt 3 + i into mod-arg form
K
khorne
Guest
is that 1cos2@ or 1+cos2@
ninetypercent
ninety ninety ninety
btw you typed the question out incorrectly, but I was able to deduce what the question was by looking at the required result 
^n \\= (1 + cos^2\Theta - sin^2\Theta + 2i sin\Theta cos\Theta)^n \\= (2cos^2\Theta + 2isin\Theta cos\Theta)^n \\= [2cos\Theta(cos\Theta + isin\Theta)]^n \\= 2^n cos^n\Theta(cosn\Theta + isinn\Theta)) By Demoivre's Theorem
By Demoivre's Theorem

