The key is to realise that what you are writing is the general term of an infinite sequence of numbers.
When you write
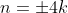
, you actually are writing the general term for n = {...,-8,-4,0,4,8,...}. In fact, since k is
any integer it doesn't matter whether we write n = 4k or n = -4k, they each generate the same sequence n = {...,-8,-4,0,4,8,...}.
This means that n = 4k and n = -4k are technically equivalent, so you could've written just n = 4k only (or n = -4k only) and that would suffice. You could even write it like n = 4(k+1) where k is an integer (i.e. replace k with k+1). This is still valid as it generates the same sequence of values n = {...,-8,-4,0,4,8,...}.
You can apply the same logic for the other part.
From your attempt on the purely imaginary part, it gives
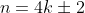
(which is correct) which represents the sequence n = {...,-10,-6,-2,2,6,10,...}.
Since
k is any integer, you could replace k with k+1 and rewrite n = 4k-2 as n = 4(k+1)-2 = 4k+2. This suggests that n = 4k-2 and n = 4k+2 are in fact equivalent as they each generate the same sequence n = {...,-10,-6,-2,2,6,10,...} so you could've just written n = 4k+2 only (or n = 4k-2 only) and that would suffice.
We also could have replaced k with -k (given k is
any integer), so you could've written n = -4k+2 only (or n = -4k-2 only). Either way, it doesn't matter which way you index it, they all represent the same sequence of numbers n = {...,-10,-6,-2,2,6,10,...}.

