Put slightly differently...
Let
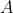
and
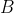
be the points such that
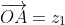
and
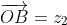
where
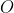
is the origin.
The locus
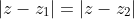
is the set of points

such that the distance from
to

and the distance from
to

are equal.
The distance from
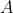
to

is
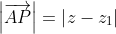
and similarly
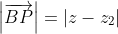
.
It is clear that
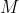
, the midpoint of
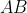
, must be one such point on the locus. The diagram provided makes it clear that the origin is another point on the locus.
Now, for any point

other than
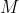
on the perpendicular bisector of
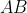
,

creates a pair of congruent triangles,
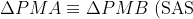})
which proves that
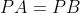
and

lies on the locus.
For any point
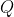
that is not on the perpendicular bisector of
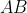
, we can prove that either
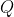
is closer to
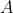
than to
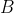
, or vice versa - that
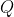
is closer to
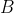
than to
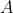
. In either case,
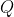
does not belong to the locus and so the locus is all points lying on the perpendicular bisector of
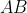
.
This result is easy to establish algebraically, by taking
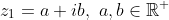
and using
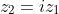
.

