HKHSCstudent
Member
- Joined
- Jun 19, 2007
- Messages
- 90
- Gender
- Undisclosed
- HSC
- 2008
- Uni Grad
- 2011
Please help me , I got stuck in the following questions!
1.
16 Koala bears were released from capavity into a wildlife park. The population P of koalas in the park t years later is given by
P=-t^3+6t^2+16,for 0<t<5
*^=power
a) after how many years was the popualtion a maximum?
b) What was the maximum population?
c)Sketch the curcve P=-t^3+6t^2+16 for 0<5<5
d) When was the population increasing most rapidly?
2. an open rectanglar box has four sides and a base, but no lid. The figure below shows the box which has dimension of 3xcm, 2xcm and a height of y cm.
(a) Write down the formulae for the outer surface area Acm^2 of the box and the volume Vcm^3 contained by the box.
(b) It is known that A+240. Elimnate y to obtain a formula V(x) for the volume as a function of x.
(c) show that x<2( (root of)10 )
(d) Find the value of x for which V is a maximum and verify the maximum value of V is 64 (root 30).
Can' t work out part (c) and (d) in question 2 .
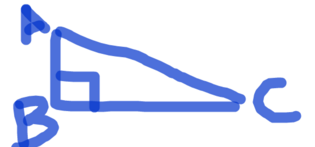
3. a piece of wire of length 5 m is bent to form the hypotenuse and side of a right-angled triangle ABC, as shown in the diagram. Let the length of the side AB be x metres.
a) What is the length of the hypotenuse AC in terms of x?
b) show that the area of the triangle ABC is 1/2 x (root of (25-10x) ) square metres.
C) What is the maximum possible area of the triangle?
4. A cylinder of radius r cm and height h cm is inscribed in a cone with base radius 3 cm and height 10cm, as in the diagram.
a) Show that the volume V of the cylinder is given by
V=(10(22/7)r^2)(3-r) ) / 3
b) Hence find the values of r and h for the cylinder which has maximum volume.
c) What is the maximum volume?
Thanks , I got struck for it a long time!!!!
1.
16 Koala bears were released from capavity into a wildlife park. The population P of koalas in the park t years later is given by
P=-t^3+6t^2+16,for 0<t<5
*^=power
a) after how many years was the popualtion a maximum?
b) What was the maximum population?
c)Sketch the curcve P=-t^3+6t^2+16 for 0<5<5
d) When was the population increasing most rapidly?
2. an open rectanglar box has four sides and a base, but no lid. The figure below shows the box which has dimension of 3xcm, 2xcm and a height of y cm.
(a) Write down the formulae for the outer surface area Acm^2 of the box and the volume Vcm^3 contained by the box.
(b) It is known that A+240. Elimnate y to obtain a formula V(x) for the volume as a function of x.
(c) show that x<2( (root of)10 )
(d) Find the value of x for which V is a maximum and verify the maximum value of V is 64 (root 30).
Can' t work out part (c) and (d) in question 2 .
3. a piece of wire of length 5 m is bent to form the hypotenuse and side of a right-angled triangle ABC, as shown in the diagram. Let the length of the side AB be x metres.
a) What is the length of the hypotenuse AC in terms of x?
b) show that the area of the triangle ABC is 1/2 x (root of (25-10x) ) square metres.
C) What is the maximum possible area of the triangle?
4. A cylinder of radius r cm and height h cm is inscribed in a cone with base radius 3 cm and height 10cm, as in the diagram.
a) Show that the volume V of the cylinder is given by
V=(10(22/7)r^2)(3-r) ) / 3
b) Hence find the values of r and h for the cylinder which has maximum volume.
c) What is the maximum volume?
Thanks , I got struck for it a long time!!!!
Last edited: