-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Differentiation (1 Viewer)
- Thread starter ISAM77
- Start date
WeiWeiMan
Well-Known Member
Height isn’t constant relative to radiusView attachment 46181
Just doing some practice on Khan Academy.
I'm just wondering why the working out on the right is wrong. If I use dV/dt = dV/dh * dh/dt , it also gives a different wrong answer. Why are these methods wrong?
I get that they're both changing over time. But why does that make them dependent on each other? e.g. you can increase the radius of a cone without changing the height of it. So the rates at which they are changing are independent are they not? Pls help me understandHeight isn’t constant relative to radius
C2H6O
alcohol𝕚𝕔
aight so in the calculation on the right, you haven’t taken into account that the height is also changing, which would obviously affect the rate of change of V. If height were constant, then the calculation on the right works. You are right that height and radius are not dependent on each other, but volume is dependent on both so you must account for both their rates of change. So with the working on the left you haveI get that they're both changing over time. But why does that make them dependent on each other? e.g. you can increase the radius of a cone without changing the height of it. So the rates at which they are changing are independent are they not? Pls help me understand
Since both r and h are dependent of t, you should use product rule, as the correct solution does. I hope this makes sense
Okaight so in the calculation on the right, you haven’t taken into account that the height is also changing, which would obviously affect the rate of change of V. If height were constant, then the calculation on the right works. You are right that height and radius are not dependent on each other, but volume is dependent on both so you must account for both their rates of change. So with the working on the left you have
Since both r and h are dependent of t, you should use product rule, as the correct solution does. I hope this makes sense
So what you're saying is, in this circumstance, dV/dt =/= dV/dr * dr/dt . Is that correct?
Would this statement be true for the question above? (I know you can't solve the question using this statement. I just want to know if the statement is true)
liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,102
- Gender
- Female
- HSC
- 2023
this is where you start getting into multivariable calculus. here volume is a function of both r and h (V(r,h)) but both of these variables also depend on time (r(t), h(t)). you can represent that with a diagram like this:Ok
So what you're saying is, in this circumstance, dV/dt =/= dV/dr * dr/dt . Is that correct?
Would this statement be true for the question above? (I know you can't solve the question using this statement. I just want to know if the statement is true)
View attachment 46185

now the multivariable chain rule basically says that in a diagram like this, to get dV/dt, you follow all paths to t and sum them up. in other words you do this:
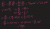
Ok, awesome! I'll keep this in mind, and will look forward to learning multivariable calculus in the futurethis is where you start getting into multivariable calculus. here volume is a function of both r and h (V(r,h)) but both of these variables also depend on time (r(t), h(t)). you can represent that with a diagram like this:
View attachment 46187
now the multivariable chain rule basically says that in a diagram like this, to get dV/dt, you follow all paths to t and sum them up. in other words you do this:
View attachment 46188


