Hi guys, I'm stuck on something trivial.
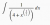 letting x = (u-4)^2
letting x = (u-4)^2
I get to the correct solution in terms of u: 2u - 8ln|u| + c
However, my confusion begins when changing the answer back to be in terms of x. Since x = (u-4)^2 , u = x^(1/2)+4 OR u =-x^(1/2)+4
So shouldn't there be two solutions in terms of x? One for the positive case and one for the negative case? Solutions across the internet and in back of book give the positive answer only. Could someone please elaborate and clear this up for me.
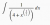 letting x = (u-4)^2
letting x = (u-4)^2I get to the correct solution in terms of u: 2u - 8ln|u| + c
However, my confusion begins when changing the answer back to be in terms of x. Since x = (u-4)^2 , u = x^(1/2)+4 OR u =-x^(1/2)+4
So shouldn't there be two solutions in terms of x? One for the positive case and one for the negative case? Solutions across the internet and in back of book give the positive answer only. Could someone please elaborate and clear this up for me.


