alussovsky
Member
- Joined
- May 17, 2018
- Messages
- 39
- Gender
- Male
- HSC
- 2019
Hi! There's a question I've been quite confused about in the Fitzpatrick textbook:
"Calculate the area bounded by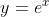 , the coordinate axes and the textbook at
, the coordinate axes and the textbook at 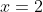 "
"
The working out I did:
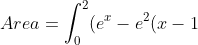) dx )
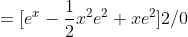
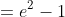
I shortened some of the working, but that was what I got. The answer to that question, however, is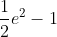
"Calculate the area bounded by
The working out I did:
I shortened some of the working, but that was what I got. The answer to that question, however, is
