Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Last edited:
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
I think LaTeX started working again:u_{n+1} = u_n +u_n ^2 and u_1 = 1/3
Find the sum from n=1 to infty of 1/(1+u_n) Latex dont work no more
Let me fix up my post thenI think LaTeX started working again:
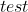
I got to :
Fixed.You might want to fix up your k's and n's.
Howd you get the second step?
Howd you get the second step?

