Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
geometric applications of calculus (1 Viewer)
- Thread starter jnney
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
We can see that x cannot be zero. Keep this in mind.
So
As
What's a number to the left of zero on the
As
What's a number to the right of zero on the
Your graph should now look like this:
http://www.mediafire.com/?sgt7c6v4ll8d28r
Horizontal asymptote:
As
As
As
Hence,
Your graph should look this this:
http://www.mediafire.com/?sgt7c6v4ll8d28r
But there's something interesting about this graph. It's very naughty.
For stationary points,
So
Test for max/min:
At
Hence
Connect your points
And finally, your graph should look like this:
http://www.mediafire.com/?4x33xdflfgb27bp
Last edited:
Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,141
- Gender
- Male
- HSC
- 2010
You mean:

You can do what SF did, or WolframAlpha if you're really stuck =P
You can do what SF did, or WolframAlpha if you're really stuck =P
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Yes, it's geometrical applications.Oh, so we don't need stationary points etc.?
No, it deals with the stationary points. When the graph cuts the horizontal asymptote and approaches infinity.It's more like a functions questions.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
I tried to explain it as easily as I can. Many of my classmates struggling with this. Pardon? I don't understand what you are asking.Oh I get it!
How about, 'For all x:y>1, y'<0, and y''>0'
Is it negative exponential?
Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,141
- Gender
- Male
- HSC
- 2010
e^(-x) goes to 0 as x goes to infinity.Oh I get it!
How about, 'For all x:y>1, y'<0, and y''>0'
Is it negative exponential?
It's probably 1 + e^(-x).
Can someone please please please help me with this pleaase
A soft drink manufacturer wants to minimise the amount of aluminium in its cans while still holding 375 mL of soft drink. Given that 375 mL has a volume of 375cm^3
a. show that the surface area of a can is given by s= 2pier^2 + 750/r
b. find the radius of the can that gives the minimum surface area.
A soft drink manufacturer wants to minimise the amount of aluminium in its cans while still holding 375 mL of soft drink. Given that 375 mL has a volume of 375cm^3
a. show that the surface area of a can is given by s= 2pier^2 + 750/r
b. find the radius of the can that gives the minimum surface area.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Wow you brought up my post haha.
First of all ALWAYS draw a pretty diagram.

Let the radius of the base of the cylinder (ie the little small circle on the bottom have a radius of r centimetres.
I will also let the height be h.
So the volume is

Now if I destroy my special can (nnoooooooooooooooooooooo), I get a net shape like this.

And the total surface area is: The area of 2 circles + the rectangle.
That is,

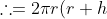)
We have now formed two equations.
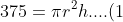)
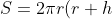....(2))
We need to eliminate a variable in order to solve these equations. I know that h looks like the odd one out, and I don't want to eliminate r because our equation we are aiming to prove contains r. It would be sensible to eliminate h!
From (1),

Substitute our new result into equation 2.
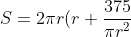)
Some simply multiplication!

YAY first part done.
This is a minimum and maximum problem, I have just constructed the equation necessary to begin solve the problem. Let's see what we can do.
I will differentiate the equation,

We know for stationary points, (min, max)



Edit: Carrotsticks has finish the problem quicker than I.
First of all ALWAYS draw a pretty diagram.

Let the radius of the base of the cylinder (ie the little small circle on the bottom have a radius of r centimetres.
I will also let the height be h.
So the volume is
Now if I destroy my special can (nnoooooooooooooooooooooo), I get a net shape like this.

And the total surface area is: The area of 2 circles + the rectangle.
That is,
We have now formed two equations.
We need to eliminate a variable in order to solve these equations. I know that h looks like the odd one out, and I don't want to eliminate r because our equation we are aiming to prove contains r. It would be sensible to eliminate h!
From (1),
Substitute our new result into equation 2.
Some simply multiplication!
YAY first part done.
This is a minimum and maximum problem, I have just constructed the equation necessary to begin solve the problem. Let's see what we can do.
I will differentiate the equation,
We know for stationary points, (min, max)
Edit: Carrotsticks has finish the problem quicker than I.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Can someone please please please help me with this pleaase
A soft drink manufacturer wants to minimise the amount of aluminium in its cans while still holding 375 mL of soft drink. Given that 375 mL has a volume of 375cm^3
a. show that the surface area of a can is given by s= 2pier^2 + 750/r
b. find the radius of the can that gives the minimum surface area.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Ah faster than I. 
- Back to English then.
- Back to English then.
